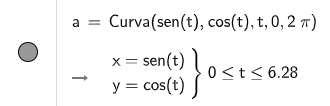
1 minute read
Son únicas las parametrizaciones de una curva
No son únicas las parametrizaciones de una curva ya que cada una se puede representar por diferentes ecuaciones paramétricas, dado que cada una tiene un diferente punto de inicio y un diferente punto de llegada en la ecuación, esto hace que varié las parametrizaciones de cada curva como se presenta en los ejemplos siguientes:
Advertisement

Ejemplo 1:

En estos ejemplos tomamos una curva simple de sin y cos. En la primera gráfica nos manejamos en intervalos 0 ≤ t ≤ 2 π, podemos observar que obtenemos un circulo completo por lo que obtenemos una parametrización única de esa gráfica. En la segunda gráfica nos manejamos en intervalos 1 ≤ t ≤ 2 π, podemos observar que la circunferencia cambia ya no es completa entonces cambia su parametrización.



Ejemplo 2:


En este ejemplo podemos observar con muncha más claridad que la parametrización es diferente en las dos gráficas de este ejemplo ya que tenemos la misma ecuación simplemente cambiamos el elemento de salida y llegada y podemos observar cómo cambia sus parámetros uno se abre más para el eje x el otro se cambia para el eje y.



