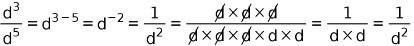
1 minute read
Producto de potencias de igual base
Otra forma de entender la división de potencias es eliminando términos comunes en el numerador y denominador, como, por ejemplo:
5) Potencia de un producto
Advertisement
También se conoce como ley distributiva de la potenciación con respecto de la multiplicación. Esta ley establece que la multiplicación (a.b.c) elevada a la n (enésima potencia) es igual a cada uno de los factores elevado a esa potencia y luego multiplicado.
Por ejemplo:
(a.b.c) n = a n . b n . c n
Esto lo podemos demostrar de la siguiente manera: (a.b.c) n = (a.b.c) (a.b.c) (a.b.c) multiplicado n veces = (a .a. a multiplicado n veces) (b. b. b multiplicado n veces) (c .c .c multiplicado n veces) = a n . b n . c n
Por ejemplo:
(2 x 3 ) 3 = 2 3 x 3 3 = (2.2.2) (3.3.3) = 8 x 27 = 216 (3ab) 2 = 3 2 . a 2 . b 2 = 9 a 2 b 2
6) Potencia de una fracción
También se conoce como ley distributiva de la potenciación respecto de la división exacta. Para elevar una fracción a una potencia, se elevan su numerador y denominador a dicha potencia de la siguiente forma:


