Estados finitos de máquinas y autómatas

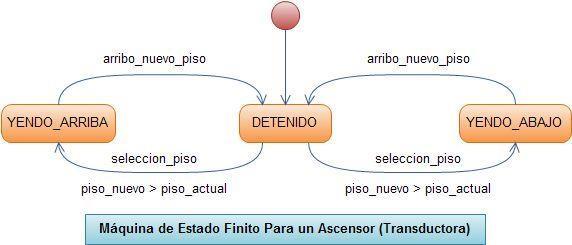
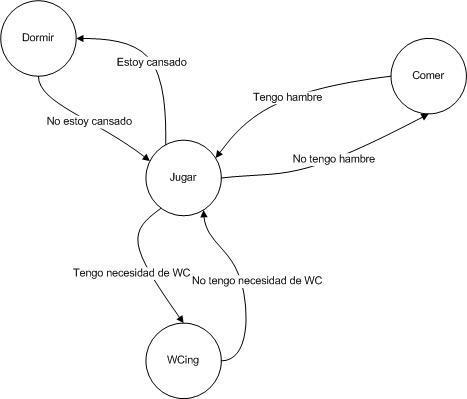
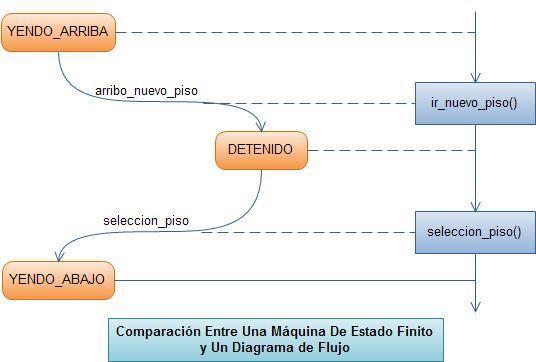
Una máquina de estado finito (FSM, Finite State Machine) o autómata finito, es una abstracción computacional que describe el comportamiento de un sistema reactivo mediante un número determinado de estados y un número determinado de transiciones entre dichos estados. Las transiciones de un estado a otro se generan en respuesta a eventos de entrada externos e internos; a su vez estas transiciones y/o subsecuentes estados pueden generar otros eventos de salida. Esta dependencia de las acciones del sistema a los eventos de entrada hace que las máquinas de estado finito (MEF) sean una herramienta adecuada para diseñar sistemas reactivos y la programación conducida por eventos (Event Driven Programming), como es el caso de la mayoría de sistemas embebidos basados en microcontroladores o microprocesadores. Las MEF se describen gráficamente mediante los llamados diagramas de estado finito (DEF), o también, diagramas de transición de estados, los cuales se encargan de representar los diferentes estados de una MEF y todas las transiciones posibles entre los estados. Las MEF no son diagramas de flujo y no deben confundirse con estos últimos. En una MEF las acciones se asocian con las flechas (transiciones), mientras que en un diagrama de flujo las acciones se asocian a los vértices de la flecha o a los bloques de proceso. Cuando una MEF está en uno de sus estados, se encuentra “en reposo” a la espera de un evento, mientras que en un diagrama de flujo el sistema se encuentra activo realizando una tarea.

Ventajas: son intuitivas y fáciles de entender, abstraen convenientemente detalles secundarios innecesarios para el análisis del sistema a un alto nivel y se enfocan en aspectos clave del mismo, aportan un componente visual que facilita el análisis y diseño del sistema, son universalmente aplicables, suelen usarse en sistemas de transmisión de datos y el uso de protocolos de comunicación, etc. Desventajas: no son aplicables a todos los problemas de diseño, no funcionan bien en sistemas con cientos o miles de estados, la adición de funcionalidad es un poco inflexible, son planas por naturaleza en el sentido de no poseer estructura definida ni permitir una jerarquización de los componentes que minimice la repetición innecesaria de otros estados, etc.

RELACIONES ENTRE EL LENGUAJE Y AUTÓMATAS

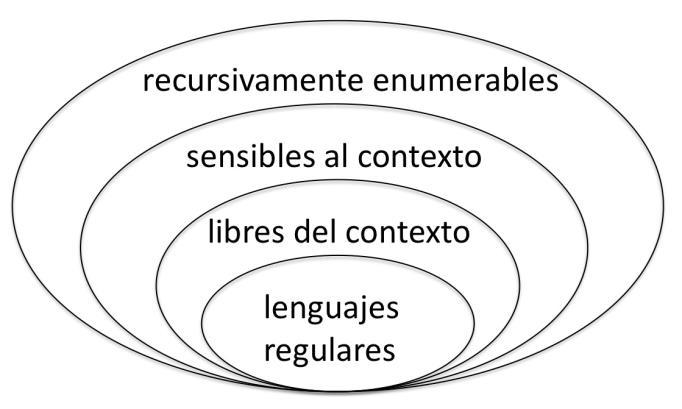
En 1956, Noam Chomsky clasificó las gramáticas en cuatro tipos de lenguajes y esta clasificación es conocida como la jerarquía de Chomsky, en la cual cada lenguaje es descrito por el tipo de gramática generado. Estos lenguajes sirven de base para clasificar lenguajes de programación. Esos cuatro tipos de lenguajes son: recursivamente enumerables, sensibles al contexto, libres de contexto y regulares, pudiendo también ser identificados respectivamente como lenguajes de tipo 0, 1, 2 y 3. Existe una correspondencia exacta entre cada uno de estos tipos de lenguajes y particulares arquitecturas de máquinas, es decir, por cada lenguaje de tipo T hay una arquitectura de máquina A que reconoce el lenguaje de tipo T y por cada arquitectura A hay un tipo T tal que todos los lenguajes reconocidos por A son de tipo T. Esta correspondencia se muestra en la tabla de la derecha.

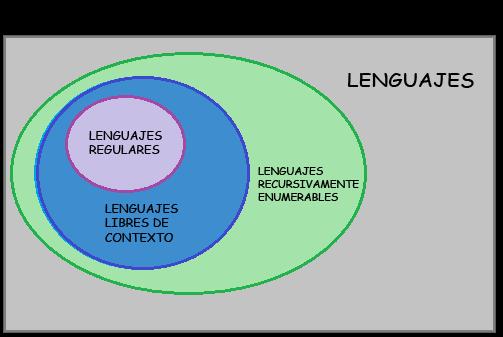
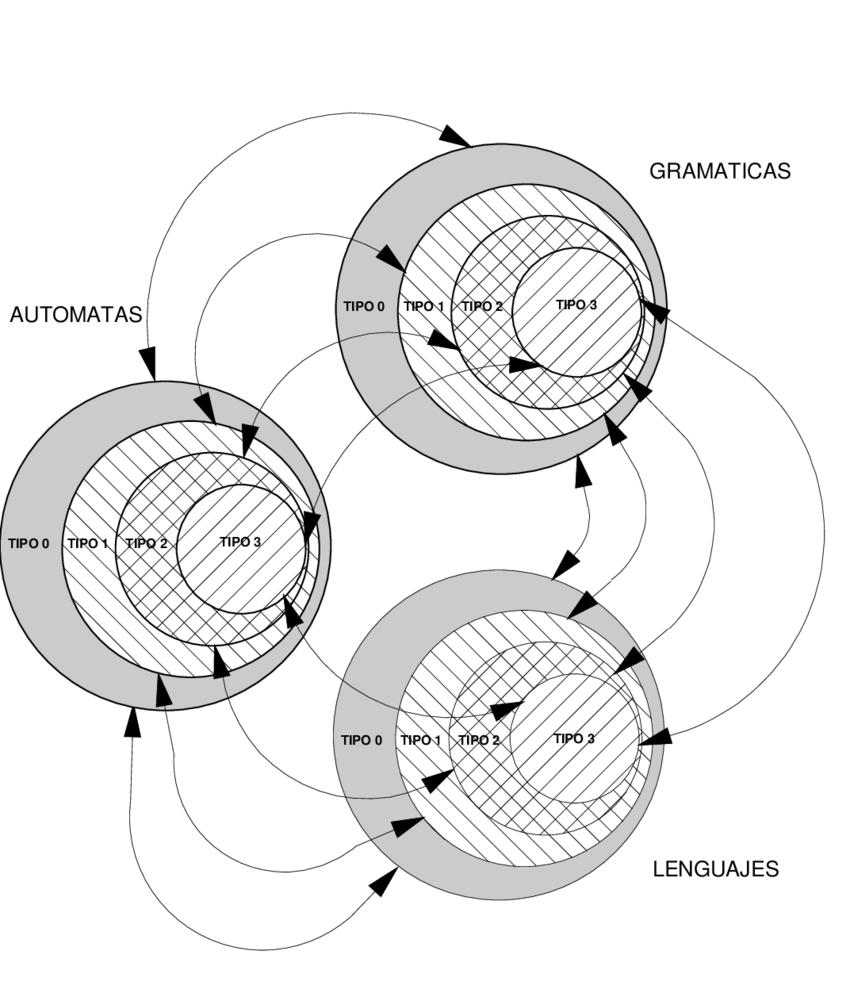
Además de la tabla, también hay un diagrama de Venn donde se muestra la relación entre los conjuntos que representan los lenguajes.

Tipo Lenguaje Tipo de máquina

0 Recursivamente enumerable 1 Sensible al contexto

Máquina de Turing Autómata linealmente acotado 2 Libre de Autómata de contexto pila 3 Regular Autómata finito y expresiones regulares

La relación entre los lenguajes se describe así: sobre un alfabeto dado, el conjunto de los lenguajes recursivamente enumerables contiene propiamente al conjunto de los lenguajes recursivos, que contiene propiamente al conjunto de los lenguajes sensibles al contexto, que a su vez contiene propiamente a los lenguajes regulares.