Business Analytics Data Analysis and Decision Making 6th Edition Albright Solutions Manual

from Business analytics data analysis and decision making 6th edition albright test bank 1

Full download at: Solution Manual: https://testbankpack.com/p/solution-manual-for-human-relations-for-career-andpersonal-success-concepts-applications-and-skills-11th-edition-dubrin-01341304059780134130408/

Test bank: https://testbankpack.com/p/test-bank-for-human-relations-for-career-and-personalsuccess-concepts-applications-and-skills-11th-edition-dubrin-01341304059780134130408/ a. There is a population regression line that joins the SDs of all possible distributions of results. b. The response variable is normally distributed. c. The standard deviation of the response variable increases as the explanatory variables increase. d. The errors are probabilistically independent.

1. Which of the following is not one of the assumptions of regression?

ANSWER: c

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-2 The Statistical Model

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

2. An error term represents the vertical distance from any point to the: a. estimated regression line b. population regression line c. value of the Y’s d. mean value of the X’s

ANSWER: b

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-2 The Statistical Model

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. It is the same as a residual. b. It can be calculated from the observed data. c. It cannot be calculated from the observed data. d. It is unbiased.

3. Which statement is true regarding regression error, ε?

ANSWER: c

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-2 The Statistical Model

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

4. The term autocorrelation refers to the observation that: a. analyzed data refers to itself b. sample is related too closely to the population c. data are in a loop (values repeat themselves) d. time series variables are usually related to their own past values

ANSWER: d

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-2 The Statistical Model

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

5. In regression analysis, multicollinearity refers to the: a. response variables being highly correlated b. explanatory variables being highly correlated c. response variable(s) and the explanatory variable(s) being highly correlated with one another d. response variables being highly correlated over time

ANSWER: b

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-2 The Statistical Model

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

6. Another term for constant error variance is: a. homoscedasticity b. heteroscedasticity c. autocorrelation d. multicollinearity

ANSWER: a

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-2 The Statistical Model

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. homoscedasticity b. heteroscedasticity c. autocorrelation d. multicollinearity

7. Time series data often exhibits which of the following characteristics?

ANSWER: c

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-2 The Statistical Model

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

8. A scatterplot that exhibits a “fan” shape (the variation of Y increases as X increases) is an example of: a. homoscedasticity b. heteroscedasticity c. autocorrelation d. multicollinearity

ANSWER: a

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-2 The Statistical Model

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. explaining the most with the least b. explaining the least with the most c. being able to explain all of the change in the response variable d. being able to predict the value of the response variable far into the future

9. Which definition best describes parsimony?

ANSWER: a

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. normal distribution b. t-distribution with n-1 degrees of freedom c. t-distribution with n-1-k degrees of freedom d. F-distribution with n-1-k degrees of freedom

10. Which of the following is the relevant sampling distribution for regression coefficients?

ANSWER: c

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis n – k - 1

11. The t-value for testing is calculated using which of the following equations?

ANSWER: d

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

12. In the standardized value , the symbol represents the: a. mean of b. variance of c. standard error of d. degrees of freedom of

ANSWER: c

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

13. The value k in the number of degrees of freedom, n-k-1, for the sampling distribution of the regression coefficients represents the: a. sample size b. population size c. number of coefficients in the regression equation, including the constant d. number of independent variables included in the equation

ANSWER: d

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

14. The appropriate hypothesis test for a regression coefficient is: a. b. c. d. none of these choices

ANSWER: b

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

15. The ANOVA table splits the total variation into two parts. They are the: a. acceptable and unacceptable variation b. adequate and inadequate variation c. resolved and unresolved variation

ANSWER: d

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

16. In regression analysis, the ANOVA table analyzes: a. the variation of the response variable Y b. the variation of the explanatory variable X c. the total variation of all variables d. all of these choices

ANSWER: a

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

17. There is evidence that the regression equation provides little explanatory power when the F-ratio: a. is large b. equals the regression coefficient c. is small d. is the constant

ANSWER: c

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

18. The appropriate hypothesis test for an ANOVA test is: a. b. c. d.

ANSWER: b

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. “wrong” values for the coefficients for the left and right foot size

19. Suppose you run a regression of a person’s height on his/her right and left foot sizes, and you suspect that there may be multicollinearity between the foot sizes. What types of problems might you see if your suspicions are true?

Copyright Cengage Learning. Powered by Cognero. Page b. large p-values for the coefficients for the left and right foot size c. small t-values for the coefficients for the left and right foot size d. all of these choices

ANSWER: d

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Comprehension

TOPICS: A-Head: 11-4 Multicollinearity

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. Look at the t-value and associated p-value. b. Check whether the t-value is less than or greater than 1.0. c. The variables are logically related to one another. d. Use economic or physical theory to make the decision. e. All of these choices are guidelines.

20. What is not one of the guidelines for including/excluding variables in a regression equation?

ANSWER: e

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-5 Include/Exclude Decisions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

21. When determining whether to include or exclude a variable in regression analysis, if the p-value associated with the variable’s t-value is above some accepted significance value, such as 0.05, then the variable: a. is a candidate for inclusion b. is a candidate for exclusion c. is redundant d. does not fit the guidelines of parsimony

ANSWER: b

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Comprehension

TOPICS: A-Head: 11-5 Include/Exclude Decisions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

22. Determining which variables to include in regression analysis by estimating a series of regression equations by successively adding or deleting variables according to prescribed rules is referred to as: a. elimination regression b. forward regression c. backward regression d. stepwise regression

ANSWER: d

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-6 Stepwise Regression

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

23. Many statistical packages have three types of equation-building procedures. They are: a. forward, linear, and non-linear b. forward, backward, and stepwise c. simple, complex, and stepwise d. inclusion, exclusion, and linear

ANSWER: b

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-6 Stepwise Regression

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

24. The objective typically used in the tree types of equation-building procedures is to: a. find the equation with a small se b. find the equation with a large R2 c. find the equation with a small se and a large R2 d. find the equation with the smallest F-ratio

ANSWER: c

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-6 Stepwise Regression

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

25. Forward regression: a. begins with all potential explanatory variables in the equation and deletes them one at a time until further deletion would do more harm than good b. adds and deletes variables until an optimal equation is achieved c. begins with no explanatory variables in the equation and successively adds one at a time until no remaining variables make a significant contribution d. randomly selects the optimal number of explanatory variables to be used

ANSWER: c

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-6 Stepwise Regression

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. an extreme value for one or more variables b. a value whose residual is abnormally large in magnitude c. values for individual explanatory variables that fall outside the general pattern of the other observations d. all of these choices

26. Which of the following would be considered a definition of an outlier?

ANSWER: d

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-7 Outliers

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

27. If you can determine that the outlier is not really a member of the relevant population, then it is appropriate and probably best to: a. average it b. reduce it c. delete it d. leave it

ANSWER: c

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-7 Outliers

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

28. A point that “tilts” the regression line toward it, is referred to as a(n): a. magnetic point b. influential point c. extreme point d. explanatory point

ANSWER: b

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-7 Outliers

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

29. When the error variance is nonconstant, it is common to see the variation increases as the explanatory variable increases (you will see a “fan shape” in the scatterplot). There are two ways you can deal with this phenomenon. These are: a. the weighted least squares and a logarithmic transformation b. the partial F and a logarithmic transformation c. the weighted least squares and the partial F d. stepwise regression and the partial F

ANSWER: a

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-8 Violations of Regression Assumptions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

30. A researcher can check whether the errors are normally distributed by using: a. a t-test or an F-test b. the Durbin-Watson statistic c. a frequency distribution or the value of the regression coefficient d. a histogram or a Q-Q plot

ANSWER: d

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-8 Violations of Regression Assumptions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. regression coefficient b. correlation coefficient c. Durbin-Watson statistic d. F-test or t-test

31. Which approach can be used to test for autocorrelation?

ANSWER: c

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-8 Violations of Regression Assumptions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

32. Residuals separated by one period that are autocorrelated indicate: a. simple autocorrelation b. redundant autocorrelation c. time 1 autocorrelation d. lag 1 autocorrelation

ANSWER: d

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-8 Violations of Regression Assumptions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

33. In regression analysis, extrapolation is performed when you: a. attempt to predict beyond the limits of the sample b. have to estimate some of the explanatory variable values c. have to use a lag variable as an explanatory variable in the model d. do not have observations for every period in the sample

ANSWER: a

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-9 Prediction

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

34. Suppose you forecast the values of all of the independent variables and insert them into a multiple regression equation and obtain a point prediction for the dependent variable. You could then use the standard error of the estimate to obtain an approximate: a. confidence interval b. prediction interval c. hypothesis test d. independence test

ANSWER: b

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-9 Prediction

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

35. The assumptions of regression are: 1) there is a population regression line, 2) the dependent variable is normally distributed, 3) the standard deviation of the response variable remains constant as the explanatory variables increase, and 4) the errors are probabilistically independent.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-2 The Statistical Model

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

36. In regression analysis, homoscedasticity refers to constant error variance.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-2 The Statistical Model

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

37. In time series data, errors are often not probabilistically independent.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-2 The Statistical Model

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

38. If exact multicollinearity exists, redundancy exists in the data.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-2 The Statistical Model

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

39. Multiple regression represents an improvement over simple regression because it allows any number of response variables to be included in the analysis.

ANSWER: False

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-6 Stepwise Regression

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

40. In a simple linear regression model, testing whether the slope of the population regression line could be zero is the same as testing whether or not the linear relationship between the response variable Y and the explanatory variable X is significant.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Comprehension

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

41. In simple linear regression, if the error variable is normally distributed, the test statistic for testing is tdistributed with n – 2 degrees of freedom.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

42. In multiple regression with k explanatory variables, the t-tests of the individual coefficients allows us to determine whether (for i = 1, 2, …., k), which tells us whether a linear relationship exists between and Y a. True b. False

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

43. In testing the overall fit of a multiple regression model in which there are three explanatory variables, the null hypothesis is .

ANSWER: False

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Comprehension

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

44. The residuals are observations of the error variable Consequently, the minimized sum of squared deviations is called the sum of squared error, labeled SSE.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

45. In a multiple regression analysis involving 4 explanatory variables and 40 data points, the degrees of freedom associated with the sum of squared errors, SSE, is 35.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Comprehension

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

46. In a simple linear regression problem, if the standard error of estimate = 15 and n = 8, then the sum of squares for error, SSE, is 1,350.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Comprehension

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

47. In regression analysis, the unexplained part of the total variation in the response variable Y is referred to as the sum of squares due to regression, SSR.

ANSWER: False

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

48. In regression analysis, the total variation in the dependent variable Y, measured by and referred to as SST, can be decomposed into two parts: the explained variation, measured by SSR, and the unexplained variation, measured by SSE.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Comprehension

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

49. The value of the sum of squares due to regression, SSR, can never be larger than the value of the sum of squares total, SST.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

50. A multiple regression model involves 40 observations and 4 explanatory variables produces SST = 1000 and SSR = 804. The value of MSE is 5.6.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Comprehension

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

51. In multiple regressions, if the F-ratio is small, the explained variation is small relative to the unexplained variation.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

52. In multiple regressions, if the F-ratio is large, the explained variation is large relative to the unexplained variation.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Comprehension

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

53. Suppose that one equation has 3 explanatory variables and an F-ratio of 49. Another equation has 5 explanatory variables and an F-ratio of 38. The first equation will always be considered a better model.

ANSWER: False

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Comprehension

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

54. In order to test the significance of a multiple regression model involving 4 explanatory variables and 40 observations, the numerator and denominator degrees of freedom for the critical value of F are 4 and 35, respectively.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Comprehension

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

55. Multicollinearity is a situation in which two or more of the explanatory variables are highly correlated with each other.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-4 Multicollinearity

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

56. When there is a group of explanatory variables that are in some sense logically related, all of them must be included in the regression equation.

ANSWER: False

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Comprehension

TOPICS: A-Head: 11-4 Multicollinearity

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True

57. In multiple regression, if there is multicollinearity between independent variables, the t-tests of the individual coefficients may indicate that some variables are not linearly related to the dependent variable, when in fact, they are.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-4 Multicollinearity

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

58. In multiple regression, the problem of multicollinearity affects the t-tests of the individual coefficients as well as the Ftest in the analysis of variance for regression, since the F-test combines these t-tests into a single test.

ANSWER: False

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-4 Multicollinearity

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

59. A backward procedure is a type of equation building procedure that begins with all potential explanatory variables in the regression equation and deletes them two at a time until further deletion would reduce the percentage of variation explained to a value less than 0.50.

ANSWER: False

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-6 Stepwise Regression

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

60. A forward procedure is a type of equation building procedure that begins with only one explanatory variable in the regression equation and successively adds one variable at a time until no remaining variables make a significant contribution.

ANSWER: False

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-6 Stepwise Regression

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

61. One of the potential characteristics of an outlier is that the value of the dependent variable is much larger or smaller than predicted by the regression line.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-7 Outliers

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

62. One method of diagnosing heteroscedasticity is to plot the residuals against the predicted values of Y, then look for a change in the spread of the plotted values.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-8 Violations of Regression Assumptions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

63. One method of dealing with heteroscedasticity is to try a logarithmic transformation of the data.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-8 Violations of Regression Assumptions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

64. The Durbin-Watson statistic can be used to test for autocorrelation.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-8 Violations of Regression Assumptions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

65. In order to estimate with 90% confidence a particular value of Y for a given value of X in a simple linear regression problem, a random sample of 20 observations is taken. The appropriate t-value that would be used is 1.734.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Comprehension

TOPICS: A-Head: 11-9 Prediction

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

66. A confidence interval constructed around a point prediction from a regression model is called a prediction interval, because the actual point being estimated is not a population parameter.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-9 Prediction

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

A carpet company, which sells and installs carpet, believes that there should be a relationship between the number of carpet installations that they will have to perform in a given month and the number of building permits that have been issued within the county where they are located. Below you will find a regression model that compares the relationship between the number of monthly carpet installations (Y) and the number of building permits that have been issued in a given month (X). The data represents monthly values for the past 10 months.

67. (A) Estimate the regression model. How well does this model fit the given data?

(B) Yes, there is a linear relationship between the number of carpet installations and the number of building permits issued at a = 0.10; The p-value = 0.0866 for the F-ratio. You can conclude that there is a significant linear relationship between these two variables.

(D) Given your answer in (C), would you recommend modifying the original regression model? If so, how would you modify it?

ANSWER:

(A) = -115076.69 + 53.469 ; since = 0.3229, building permits (X) explains about one-third of the variations in monthly carpet installations (Y), but the carpet company may want to include other variables to get a better model.

(C) The Durbin-Watson statistic = 1.2183 seems to indicate that there is lag 1 autocorrelation present in this data. This value indicates positive autocorrelation in the data.

(D) There is not an easy fix to the autocorrelation problem. In this case, you could use the number of permits issued in a given month to determine the carpet installations for the next month. Also, you could look for other variables that may affect carpet installations, such as interest rates (affecting construction), population, new businesses, etc. You may be able to identify another variable that has a linear relationship with carpet installations.

POINTS: 1

DIFFICULTY: Moderate | Bloom’s: Application

TOPICS: A-Head: 11-8 Violations of Regression Assumptions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

68. Below you will find a scatterplot of data gathered by an online retail company. The company has been able to obtain the annual salaries of their customers and the amount that each of these customers spent on the company's site last year. Based on the scatterplot below, would you conclude that these data meet all four assumptions of regression? Explain your answer.

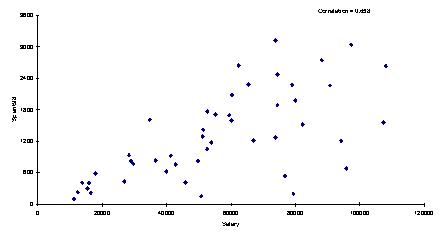
ANSWER: The assumption that the variation of the Y’s about the regression line is the same regardless of the value of the X’s (homoscedasticity) seems to be violated. The fan shape pattern in the graph seems to exhibit what can be describes as heteroscedasticity or nonconstant error variance.

POINTS: 1

DIFFICULTY: Moderate | Bloom’s: Application

TOPICS: A-Head: 11-8 Violations of Regression Assumptions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

The owner of a pizza restaurant chain would like to predict the sales of her recent specialty, a Mediterranean flatbread pizza. She has gathered data on monthly sales of the Mediterranean flatbread pizza at her restaurants. She has also gathered information related to the average price of flatbread pizzas, the monthly advertising expenditures, and the disposable income per household in the areas surrounding the restaurants. Below you will find output from the stepwise regression analysis. The p-value method was used with a cutoff of 0.05.

Summary measures

69. (A) Summarize the findings of the stepwise regression method using this cutoff value.

(B) When the cutoff value was increased to 0.10, the output below was the result. The table at top left represents the change when the disposable income variable is added to the model and the table at top right represents the average price variable being added. The regression model with both added variables is shown in the bottom table. Summarize the results for this model.

(A) When a cutoff value of 0.05 is used, the only explanatory variable that is included in the model is the monthly advertising expenditures variable. The model is = -45233.64+ 1.972 This model indicates that when an additional dollar of advertising is spent, the monthly sales increase on average by $1.97.

(B) When a cutoff value of 0.10 is used, all three explanatory variables are included in the model. The new model is now =-73971.53 + 0.952 + 2.606 – 2056.27 This model indicates that a one dollar increase in advertising will increase sales by $0.95. As the disposable income increases by one dollar the sales will increase by $2.61 and as the average price increases by one dollar the sales will decrease by $2056.27. In each case, all variables, except the one we are interpreting its coefficient, are held constant.

(C) It seems that there is some increased benefit by using the second (expanded) model. In going from the first to the second model, there is an increase in the value (from 0.9049 to 0.9454) and a decrease in the se value (from 3924.53 to 3179.03, a decrease of approximately 20%). The second model seems to be stronger. However, based on the principle of parsimony, you could make an argument for using the first regression equation.

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Application

TOPICS: A-Head: 11-6 Stepwise Regression

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

The information below represents the relationship between the selling price (Y, in $1,000) of a home, the square footage of the home ( ), and the number of rooms in the home ( ). The data represents 60 homes sold in a particular area of East Lansing, Michigan and was analyzed using multiple linear regression and simple regression for each independent variable. The first two tables relate to the multiple regression analysis.

Regression coefficients

The following table is for a simple regression model using only size ( = 0.8812)

The following table is for a simple regression model using only number of rooms ( = 0.3657)

70. (A) Use the information related to the multiple regression model to determine whether each of the regression coefficients are statistically different from 0 at a 5% significance level. Summarize your findings.

(B) Test at the 5% significance level the relationship between Y and X in each of the simple linear regression models. How does this compare to your answer in (A)? Explain.

ANSWER:

(A) Given a p-value = 0 < =.05, we reject that and conclude that is statistically different from 0. Given a p-value = 0.5336 > = .05, we fail to reject that = 0 and conclude that is not statistically different from 0. These results indicate that the size of the home is significant in predicting the selling price, but the number of rooms is not.

(B) Given a p-value = 0 < = .05, we reject that and conclude that is statistically different from 0. Given a p-value = 0.0169 < = .05, we reject that and conclude that is statistically different from 0. Thus, when analyzing each simple regression model independently, the results show that each variable is statistically significant. However, the multiple regression model shows that (size in square feet) is statistically significant while (number of rooms) is not.

(C) These results seem to be an indication of multicollinearity. Each variable is statistically significant on its own, but not when used together. You would also expect that the variables size of the home and number of rooms would be closely associated with one another.

POINTS: 1

DIFFICULTY: Moderate | Bloom’s: Analysis

TOPICS: A-Head: 11-4 Multicollinearity

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

An Internet-based retail company that specializes in audio and visual equipment is interested in creating a model to determine the amount of money, in dollars, its customers will spend purchasing products from them in the coming year. In order to create a reliable model, this company has tracked a number of variables on its customers. Below you will find the Excel output related to several of these variables. This company has tried using the customer’s annual salary for entire household , the number of children in the household , and if the customer purchased merchandise from them in the previous year ( in 2015).

71. (A) Estimate the regression model. How well does this model fit the data?

(B) Is there a linear relationship between the explanatory variables and the dependent variable? Explain how you arrived at your answer at the 5% significance level.

(C) Use the estimated regression model to predict the amount of money a customer will spend if their annual salary is $45,000, they have 1 child and they were a customer that purchased merchandise in the previous year (2015).

(D) Find a 95% prediction interval for the point prediction calculated in (C) Use a t-multiple = 2.02.

(E) Find a 95% confidence interval for the amount of money spent by all customers sharing the characteristics described in (C). Use a t-multiple = 2.02.

(F) How do you explain the differences between the widths of the intervals in (D) and (E)?

ANSWER:

(A) = 291.243 + 0.026 – 331.972 + 281.80 ; this is a good fitting model. The = 0.6122 and the adjusted = 0.5852.

(B) , At least one is different from 0. Since the p-value = 0.0000 < =.05 for the F-ratio, you reject and conclude that there is a significant linear relationship between these three explanatory variables and the dependent variable.

(D) Since the standard error of prediction for a single Y is approximately equal to the standard error of estimate , then the prediction interval is: Y± t –multiple * se) = ($316.84, $2,505.3)

(E) Since the standard error of prediction for the mean of Y (denoted by ) is approximately equal to the standard error of estimate divided by the square root for the sample size, then the confidence interval is

(F) The prediction interval (D) is much wider than the confidence interval (E). The prediction interval is just for one point and because of the rather large standard error (se = 541.70) we obtain a wider interval. The confidence interval is for the mean value of Y and the standard error is reduced by the .

POINTS: 1

DIFFICULTY: Challenging | Bloom’s: Application

TOPICS: A-Head: 11-9 Prediction

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

A company that makes baseball caps would like to predict the sales of its main product, standard little league caps. The company has gathered data on monthly sales of caps at all of its retail stores, along with information related to the average retail price, which varies by location. Below you will find regression output comparing these two variables.

72. (A) Estimate the regression model. How well does this model fit the given data?

(B) Is there a linear relationship between X and Y at the 5% significance level? Explain how you arrived at your answer.

(C) Use the estimated regression model to predict the number of caps that will be sold during the next month if the average selling price is $10.

(D) Find a 95% prediction interval for the number of caps determined in (C). Use t- multiple = 2.

(E) Find a 95% confidence interval for the average number of caps sold given an average selling price of $10. Use a tmultiple = 2.

(F) How do you explain the differences between the widths of the intervals in (D) and (E)?

ANSWER:

(A) = 147984.44 + -7370.94 ; since = 0.3472, average price (X) explains about one-third of the variations in sales (Y), although the company may want to include other variables to get a better model.

(B) Since the p-value = 0.0101 < = .05 for the F-ratio, you reject that and conclude that there is a significant linear relationship between these two variables.

(D) Since the standard error of prediction for a single Y is approximately equal to the standard error of estimate , then the prediction interval is 74,275 ± (2 x 10,283.97) = 74,275 20,567.94 = (53,707.06, 94,842.94).

(E) Since the standard error of prediction for the mean of Y (denoted by ) is approximately equal to the standard error of estimate divided by the square root of the sample size, then the confidence interval is: 74,275 ± (2)(10,283.97 / ) = 74,275 4,847.9 = (69,427.1, 79,122.9).

(F) The prediction interval (D) is much wider than the confidence interval (E) The prediction interval is just for one point and because of the rather large standard error (se = 10,283.97) we get a rather wide

Copyright Cengage Learning. Powered by Cognero. Page interval. The confidence interval is for the mean value of Y and the error is reduced by the

POINTS: 1

DIFFICULTY: Challenging | Bloom’s: Application

TOPICS: A-Head: 11-9 Prediction

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

A local truck rental company wants to use regression to predict the yearly maintenance expense (Y), in dollars, for a truck using the number of miles driven during the year and the age of the truck in years at the beginning of the year. To examine the relationship, the company has gathered the data on 15 trucks and regression analysis has been conducted. The regression output is presented below.

73. (A) Estimate the regression model. How well does this model fit the given data?

(B) Is there a linear relationship between the two explanatory variables and the dependent variable at the 5% significance level? Explain how you arrived at your answer.

(C) Use the estimated regression model to predict the annual maintenance expense of a truck that is driven 14,000 miles per year and is 5 years old.

(D) Find a 95% prediction interval for the maintenance expense determined in (C). Use a t-multiple = 2.

(E) Find a 95% confidence interval for the maintenance expense for all trucks sharing the characteristics provided in (C). Use a t-multiple = 2.

(F) How do you explain the differences between the widths of the intervals in (D) and (E)?

ANSWER:

(A) = -680.70 + 0.080 + 44.238 ; this is a good fitting model. The = 0.8665 and the adjusted = 0.8442.

(B) , At least one is different from 0 Since the p-value = 0.0000 < = .05 for the F-ratio, you reject and conclude that there is a significant linear relationship between these variables.

(D) Since the standard error of prediction for a single Y is approximately equal to the standard error of estimate , then the prediction interval is: 660.45 ± (2)(87.397) = 660.45 174.79 =($485.65, $835.24).

(E) Since the standard error of prediction for the mean value of Y (denoted by ) is approximately equal to the standard error of estimate divided by the square root of the sample size, then the confidence interval is:

= 660.49 ± (2)(87.397 / ROOT15) = 660.49 ± 45.13 = ($615.36, $705.62)

(F) The prediction interval (D) is much wider than the confidence interval (E). The prediction interval is just for one point and because of the rather large standard error (se = 87.397) we get a rather wide interval. The confidence interval is for the mean value of Y and the error is reduced by the .

POINTS: 1

DIFFICULTY: Challenging | Bloom’s: Application

TOPICS: A-Head: 11-9 Prediction

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

A new online auction site specializes in selling automotive parts for classic cars. The founder of the company believes that the price received for a particular item increases with its age (i.e., the age of the car on which the item can be used in years) and with the number of bidders. The Excel multiple regression output is shown below.

74. (A) Estimate a multiple regression model for the data.

(B) Which of the variables in this model have regression coefficients that are statistically different from 0 at the 5% significance level?

(C) Given your findings in (B), which variables, if any, would you choose to remove from the model estimated in (A)? Explain your decision.

ANSWER:

(A) = - 1242.99 + 75.017 + 13.973

(B) Given a p-value = 0.0 < = .05, we reject that and conclude that is statistically different from 0. Given a p-value = 0.194 > = .05, we fail to reject that and conclude that is not statistically different from 0.

(C) The results in (B) indicate that the regression coefficient of - the number of bidders - is not significantly different from 0. Therefore, you can remove this variable from the model in (A) and still have a strong model to predict the selling price Y using - the age of item used.

POINTS: 1

DIFFICULTY: Challenging | Bloom’s: Application

TOPICS: A-Head: 11-5 Include/Exclude Decisions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

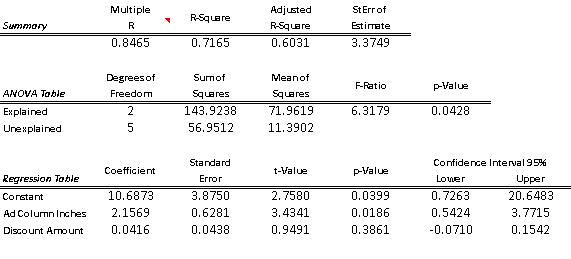
The owner of a large chain of health spas has selected eight of her smaller clubs for a test in which she varies the size of the newspaper ad , and the amount of the initiation fee discount to see how this might affect the number of prospective members who visit each club during the following week. The results are shown in the table below:

The results of a multiple regression analysis are below.

75. (A) Determine the least-squares multiple regression equation.

(B) Interpret the Y-intercept of the regression equation.

(D) What is the estimated number of new visitors to a club if the size of the ad is 6 column-inches and a $100 discount is offered?

(E) Determine the approximate 95% prediction interval for the number of new visitors to a given club when the ad is 5 column-inches and the discount is $80.

(F) What is the value for the percentage of variation explained, and exactly what does it indicate?

(G) At the 0.05 level, is the overall regression equation in (A) significant?

(H) Use the 0.05 level in concluding whether each partial regression coefficient differs significantly from zero.

(I Interpret the results of the preceding tests in (H) and (I) in the context of the two explanatory variables described in the problem.

(J) Construct a 95% confidence interval for each partial regression coefficient in the population regression equation.

ANSWER:

(A) Visitors = 10.687 + 2.1569 Ad Size + 0.04157 Discount.

(B) The Y-intercept indicates that about 10 or 11 visitors (namely; 10.687) would come to the clubs if there were neither ads nor discounts.

(C) The partial regression coefficient for the ad data indicates that, holding the level of the discount constant, increasing the ad size by one column inch will bring in just over 2 new visitors. The partial regression coefficient for the discount data indicates that, holding the size of the ad constant, an additional $1 discount will add 0.04157 to the number of visitors.

(D) Estimated number of new visitors = 10.687 + 2.1569(6) + 0.04157(100) = 27.785.

(E) The corresponding approximate 95% prediction interval is:

(F) The percentage of variation explained = 0.7165. This indicates that 71.65% of the variation in the number of new visitors to the club is explained by the regression equation.

(G) The appropriate null and alternative hypotheses are: vs. At least one is different from 0. The p-value for the ANOVA test of the overall significance of the regression equation is 0.0428. Since p-value = 0.0428 < = 0.05, we reject the null hypothesis. At this level, there is evidence to suggest that the regression equation is significant.

(H) Here we are asked to conduct two hypothesis tests. We will not test the Y-intercept since this test is generally not of practical importance. The appropriate null and alternative hypotheses are: and The p-value for the test of is 0.0186. Since p-value = 0.3861 > = 0.05 we do NOT reject the null hypothesis. At this level, there is evidence to suggest that is nonzero. The p-value for the test of is 0.3861. Since p-value = 0.3861 > = 0.05, we reject the null hypothesis. At this level, there is no evidence to suggest that is nonzero.

(I) The ANOVA test for the overall regression in (H) indicates that the regression explains a significant proportion of the variation in the number of new visitors to the club. The tests for the individual partial regression coefficients in (I) indicate that the size of the ad contributes to the explanatory power of the model, while the discount offered does not.

(J) With d.f. = 8 - 2 - 1 = 5, the appropriate t-multiple for the 95% confidence interval will be 2.571. The 95% confidence interval for population partial regression coefficient is:

2.1569 ± 2.571(0.6281) = 2.1569 ± 1.6148 = (0.5421, 3.7717)

The 95% confidence interval for population partial regression coefficient is:

0.04157 ± 2.571(0.0438) = 0.04157±0.1126 = (-0.0710, 0.1542)

With Excel® , we can obtain confidence intervals for the population regression coefficients along with the standard regression output. Excel® will provide 95% confidence intervals, but we can also specify the inclusion of 90% or any other confidence levels we wish to see.

POINTS: 1

DIFFICULTY: Challenging | Bloom’s: Application

TOPICS: A-Head: 11-5 Include/Exclude Decisions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

Many companies manufacture products that are at least partially produced using chemicals (for example, paint). In many cases, the quality of the finished product is a function of the temperature and pressure at which the chemical reactions

Copyright Cengage Learning. Powered by Cognero. Page 26 take place. Suppose that a particular manufacturer in Texas wants to model the quality (Y) of a product as a function of the temperature and the pressure at which it is produced. The table below contains data obtained from a designed experiment involving these variables. Note that the assigned quality score can range from a minimum of 0 to a maximum of 100 for each manufactured product.

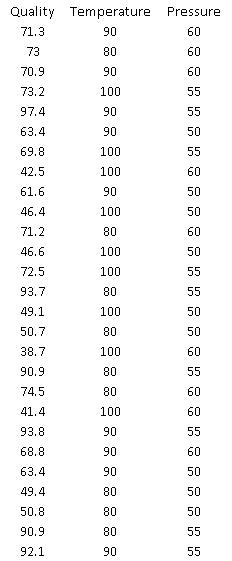
76. (A) Estimate a multiple regression model that includes the two given explanatory variables. Assess this set of explanatory variables with an F-test, and report a p-value.

(B) Identify and interpret the percentage of variance explained for the model in (A).

(D) Which regression equation is the most appropriate one for modeling the quality of the given product? Bear in mind that a good statistical model is usually parsimonious.

ANSWER: (A)

The p-value associated with the F-test in this ANOVA table is right around 0.06, so we would probably say that these two variables may have some significant explanatory power.

(B) The percentage of variance explained is 0.2115, which suggests that about 21% of the variation of quality of the manufactured product is explained by the model

= 106.0852 – 0.9161(Temperature) + 0.7878 (Pressure)

(C) The percentage of variance explained is 0.9930, which suggests that about 99% of the variation of quality of the manufactured product is explained by the model

= -5127.8991+ 31.0964 (Temperature) + 139.7472 (Pressure) -0.1334 (Temperature) - 1.1442 (Pressure) - 0.1455 (Temperature) (Pressure)

(D) Even with parsimony in mind, the equation from (B) is definitely preferred over the equation from (A).

POINTS: 1

DIFFICULTY: Challenging | Bloom’s: Application

TOPICS: A-Head: 11-3 Inferences About the Regression Coefficients

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

A manufacturing firm wants to determine whether a relationship exists between the number of work-hours an employee misses per year (Y) and the employee’s annual wages (X), to test the hypothesis that increased compensation induces better work attendance. The data provided in the table below are based on a random sample of 15 employees from this organization.

77. (A) Estimate a simple linear regression model using the sample data. How well does the estimated model fit the sample data?

(B) Perform an F-test for the existence of a linear relationship between Y and X Use a 5% level of significance.

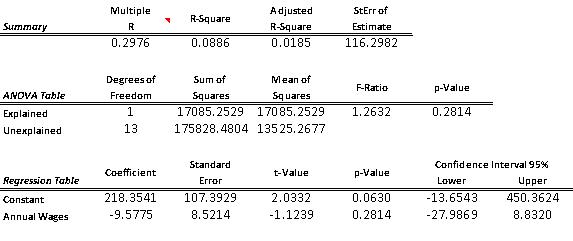
(D) How do you explain the results you have found in (A) through (C)?

(E) Suppose you learn that the 10th employee in the sample has been fired for missing an excessive number of workhours during the past year. In light of this information, how would you proceed to estimate the relationship between the number of work-hours an employee misses per year and the employee’s annual wages, using the available information? If you decide to revise your estimate of this regression equation, repeat (A) and (B)

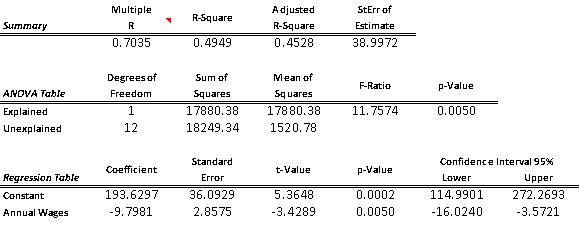
ANSWER: (A) simple linear regression model is =218.35 – 9.5775 (Annual Wages). The fit of this estimated model is pretty poor; the percent variation explained is only 0.0886.

(B) Since the p-value = 0.2814 is well above 0.05, this indicates that there is no linear relationship between Y (work hours missed) and X (employee’s annual wages).

(C)

Copyright Cengage Learning. Powered by Cognero. Page simple linear regression model is =193.6 – 9.79 (Annual Wages). The fit of this estimated model is much better than the one obtained in (A). The percentage of variation explained has improved from only 0.0886 to 0.4949. In addition, with the revised model, the p-value = 0.005 is well below 0.05, which indicates that there is a linear relationship between Y (work hours missed) and X (employee’s annual wages). This also confirms what we expect to see, intuitively; as wages increase, worker hours missed decreases (i.e., slope is negative)

The chart of residuals versus fitted values points to an obvious outlier associated with the 10th employee in the sample who has missed 485 hours of work (for this employee, fitted value = 101.5 and residual = 383.5).

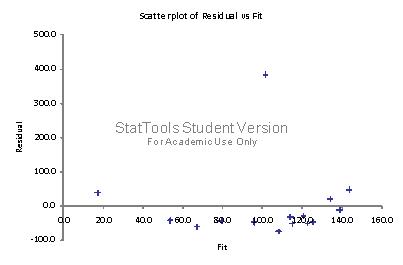
(D) Since there is no evidence of a linear relationship between X and Y, and the existence of an obvious outlier, the estimated linear regression model in (A) provides a very poor fit to the data.

(E) We should eliminate the data point associated with this employee and rerun the regression in (A) and (B). We expect to obtain much better results.

POINTS: 1

DIFFICULTY: Challenging | Bloom’s: Application

TOPICS: A-Head: 11-7 Outliers

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

The manager of a commuter rail transportation system is asked by his governing board to predict the demand for rides in the large city served by the transportation network. The system manager has collected data on variables thought to be related to the number of weekly riders on the city’s rail system. The table shown below contains these data.

The variables “weekly riders” and “population” are measured in thousands, and the variables “price per ride”, “income”, and “parking rate” are measured in dollars.

78. (A) Estimate a multiple regression model using all of the available explanatory variables.

(B) Conduct and interpret the result of an F- test on the given model. Employ a 5% level of significance in conducting this statistical hypothesis test.

ANSWER: (A)

Copyright Cengage Learning. Powered by Cognero. Page 31 multiple regression model (where Y is the weekly riders) that includes all of the explanatory variables, excluding time (i.e., year) is given by:

= 124.4 – 166.9(Price/ride) + 0.62(Population) - 0.047(Income) + 194.7(Parking rate)

(B) Since the p-value for the F- test of this model essentially equals zero (see ANOVA Table in A), we can conclude that this set of explanatory variables is useful in explaining the variation in Weekly Riders.

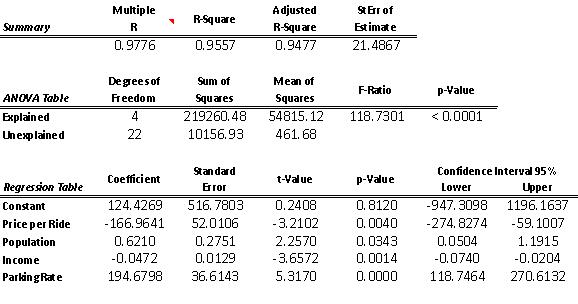
(C) The time series plot of residuals and value of the Durbin-Watson statistic which, using the function =StatDurbinWatson, is 1.41, indicate some positive autocorrelation, but not enough to be overly concerned.

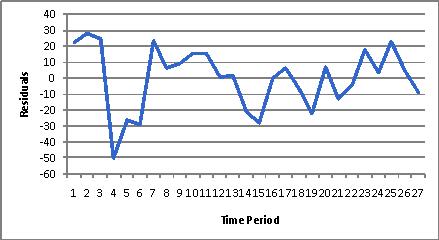
POINTS: 1

DIFFICULTY: Challenging | Bloom’s: Application

TOPICS: A-Head: 11-8 Violations of Regression Assumptions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

79. Do you see any problems evident in the plot below of residuals versus fitted values from a multiple regression analysis? Explain your answer.

ANSWER: There are a few points with large positive and negative residuals, but there is no obvious pattern or trend in the residuals, so there is no major problem evident.

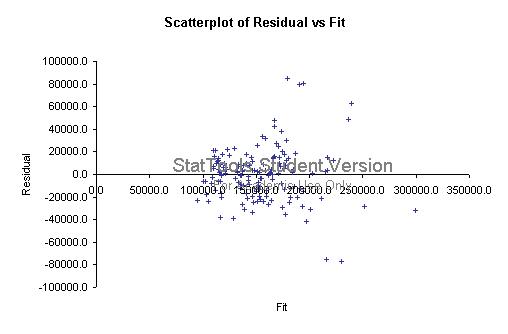
POINTS: 1

DIFFICULTY: Challenging | Bloom’s: Application

TOPICS: A-Head: 11-8 Violations of Regression Assumptions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. There is a population regression line. b. The response variable is not normally distributed. c. The response variable is normally distributed. d. The errors are probabilistically independent.

80. Which of the following is not one of the assumptions of regression?

ANSWER: b

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-2 The Statistical Model

OTHER: BUSPROG: Analytic | DISC: Regression Analysis a. True b. False

81. Heteroscedasticity means that the variability of Y values is larger for some X values than for others.

ANSWER: True

POINTS: 1

DIFFICULTY: Easy | Bloom’s: Knowledge

TOPICS: A-Head: 11-8 Violations of Regression Assumptions

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

82. Homoscedasticity means that the variability of Y values is the same for all X values.

OTHER: BUSPROG: Analytic | DISC: Regression Analysis

This article is from:

Business analytics data analysis and decision making 6th edition albright test bank 1