Datos agrupados

Los datos agrupados son aquellos que se han clasificado en categorías o clases, tomando como criterio su frecuencia. Esto se hace con la finalidad de simplificar el manejo de grandes cantidades de datos y establecer sus tendencias. Una vez organizados en estas clases por sus frecuencias, los datos conforman una distribución de frecuencias, de la cual se extrae información de utilidad a través de sus características.

A continuación, veremos un ejemplo sencillo de datos agrupados: Supongamos que se mide la estatura de 100 estudiantes de sexo femenino, seleccionadas de entre todos los cursos de física básica de una universidad, y se obtienen los siguientes resultados:

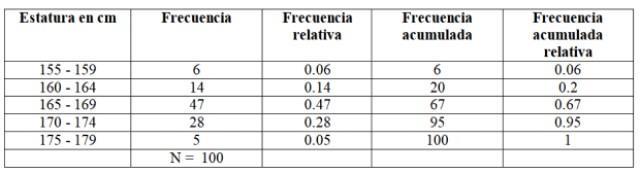
Los resultados obtenidos se dividieron en 5 clases, que aparecen en la columna izquierda. La primera clase, comprendida entre 155 y 159 cm, tiene 6 estudiantes, la segunda clase 160 – 164 cm tiene 14 estudiantes, la tercera clase de 165 a 169 cm es la que tiene el mayor número de integrantes: 47. Luego sigue la clase de 170-174 cm con 28 alumnas y por último la de 175 a 179 cm con apenas 5. El número de integrantes de cada clase es precisamente la frecuencia o frecuencia absoluta y al sumarlas todas, se obtiene el total de datos, que en este ejemplo es 100.

Caracteristicas de la distribución de Frecuencias Frecuencia

Como hemos visto, la frecuencia es el número de veces que se repite un dato. Y para facilitar los cálculos de las propiedades de la distribución, tales como la media y la varianza, se definen las siguientes cantidades: Frecuencia acumulada: se obtiene sumando la frecuencia de una clase con la frecuencia acumulada anterior. La primera de todas las frecuencias coincide con la del intervalo en cuestión, y la última es el número total de datos. Frecuencia relativa: se calcula dividiendo la frecuencia absoluta de cada clase entre el número total de datos. Y si se multiplica por 100 se tiene la frecuencia relativa porcentual. Frecuencia relativa acumulada: es la suma de las frecuencias relativas de cada clase con el acumulado anterior. La última de las frecuencias relativas acumuladas debe ser igual a 1. Para nuestro ejemplo, las frecuencias quedan así:

Limites

Los valores extremos de cada clase o intervalo se llaman límites de clase. Como podemos ver, cada clase tiene un límite menor y uno mayor. Por ejemplo, la primera clase del estudio acerca de las estaturas tiene un límite menor de 155 cm y uno mayor de 159 cm. Este ejemplo tiene límites que están claramente definidos, sin embargo, es posible definir límites abiertos: si en vez de definir los valores exactos, se dijese “estatura menor a 160 cm”, “estatura menor a 165 cm” y así sucesivamente.

Fronteras

La estatura es una variable continua, por lo que se puede considerar que la primera clase en realidad comienza en 154.5 cm, ya que, al redondear este valor al entero más cercano, se obtiene 155 cm. Esta clase abarca todos los valores hasta 159.5 cm, porque a partir de este, las estaturas se redondean a 160.0 cm. Una estatura de 159.7 cm ya pertenece a la siguiente clase. Las fronteras de clase reales de este ejemplo son, en cm:

154.5 – 159.5 159.5 – 164.5 164.5 – 169.5 169.5 – 174.5 174.5 – 179.5

Amplitud

La amplitud de una clase se obtiene restando las fronteras. Para el primer intervalo de nuestro ejemplo se tiene 159.5 – 154.5 cm = 5 cm. El lector puede comprobar que para los demás intervalos del ejemplo la amplitud también resulta de 5 cm. Sin embargo, es de hacer notar que se pueden construir distribuciones con intervalos de distinta amplitud.

Marca de clase

Es el punto de medio del intervalo y se obtiene mediante el promedio entre el límite superior y el límite inferior. Para nuestro ejemplo, la primera marca de clase es (155 + 159) /2 = 157 cm. El lector puede comprobar que las restantes marcas de clase son: 162, 167, 172 y 177 cm.

Determinar las marcas de clase es importante, pues son necesarias para encontrar la media aritmética y la varianza de la distribución.

Las medidas de tendencia central más utilizadas son la media, la mediana y la moda, y describen precisamente la tendencia de los datos a agruparse alrededor de cierto valor central.

Media

Es una de las principales medidas de tendencia central. En los datos agrupados se puede calcular la media aritmética mediante la fórmula:

-X es la media -fi es la frecuencia de la clase -mi es la marca de clase -g es el número de clases -n es el número total de los datos

Medidas de tendencia central y dispersión

Para la mediana hay que identificar el intervalo donde se encuentra la observación n/2. En nuestro ejemplo esta observación es la número 50, porque hay un total de 100 datos. Dicha observación está en el intervalo 165-169 cm. Después hay que interpolar para encontrar el valor numérico que corresponde a esa observación, para lo cual se emplea la fórmula:

Donde:

Mediana

-c = ancho del intervalo donde se encuentra la mediana -BM = la frontera inferior del intervalo al que pertenece la mediana -fm = cantidad de observaciones que contiene el intervalo de la mediana -n/2 = mitad del total de datos -fBM = número total de observaciones antes del intervalo de la mediana

Medidas de tendencia central y dispersión

Moda

Para la moda se identifica la clase modal, aquella que contiene la mayoría de las observaciones, cuya marca de clase es conocida.

Varianza y desviación estándar

La varianza y la desviación estándar son medidas de dispersión. Si denotamos la varianza con s2 y a la desviación estándar, que es la raíz cuadrada de la varianza como s, para datos agrupados tendremos respectivamente:

Y

Los cuartiles son una herramienta que usamos en la estadística y que nos sirve para administrar grupos de datos previamente ordenados. Los cuartiles son los tres valores de la variable que dividen a un conjunto de datos ordenados en cuatro partes iguales.

y determinan los valores correspondientes al % de los datos. coincide con la mediana. %, al % y al

Cuartiles

Cálculo de los cuartiles para datos agrupados

En primer lugar, buscamos la clase donde se encuentra la tabla de las frecuencias acumuladas.

, en

es el límite inferior de la clase donde se encuentra el cuartil.

es la suma de las frecuencias absolutas.

es la frecuencia acumulada anterior a la clase del cuartil.

es la amplitud de la clase.

Asimetrías Coeficiente de asimetría de Fisher

El coeficiente de asimetría de Fisher CAF evalúa la proximidad de los datos a su media x. Cuanto mayor sea la suma ∑(xi–x)3, mayor será la asimetría. Sea el conjunto X= (x1, x2, …, xN), entonces la fórmula de la asimetría de Fisher es:

Cuando los datos están agrupados o agrupados en intervalos, la fórmula del coeficiente de asimetría de Fisher se convierte en:

Si CAF<0: la distribución tiene una asimetría negativa y se alarga a valores menores que la media. Si CAF=0: la distribución es simétrica.

Si CAF>0: la distribución tiene una asimetría positiva y se alarga a valores mayores que la media.

Coeficiente de asimetría de Pearson

El coeficiente de asimetría de Pearson CAP mide la diferencia entre la media y la moda respecto a la dispersión del conjunto X=(x1, x2,…, xN). Este procedimiento, menos usado, lo emplearemos solamente en distribuciones unimodales y poco asimétricas.

Si CAP<0: la distribución tiene una asimetría negativa, puesto que la media es menor que la moda. Si CAP=0: la distribución es simétrica.

Si CAP>0: la distribución tiene una asimetría positiva, ya que la media es mayor que la moda.

Coeficiente de asimetría de Bowley

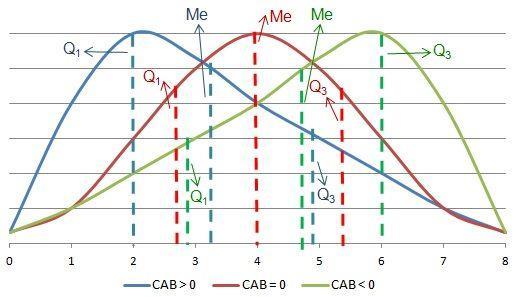
El coeficiente de asimetría de Bowley CAB toma como referencia los cuartiles para determinar si la distribución es simétrica o no. Para aplicar este coeficiente, se supone que el comportamiento de la distribución en los extremos es similar. Sea el conjunto X= (x1, x2, …, xN), la asimetría de Bowley es:

Esta fórmula viene de:

Recordemos que la mediana (Me) es lo mismo que el segundo cuartil (Q2).

Por lo que la fórmula del coeficiente de asimetría de Bowley también se puede escribir así:

Si CAB<0: la distribución tiene una asimetría negativa, puesto que la distancia de la mediana al primer cuartil es mayor que al tercero. Si CAB=0: la distribución es simétrica, ya que el primer y tercer cuartil están a la misma distancia de la mediana.

Si CAB>0: la distribución tiene una asimetría positiva, ya que la distancia de la mediana al tercer cuartil es mayor que al primero.

Curtosis

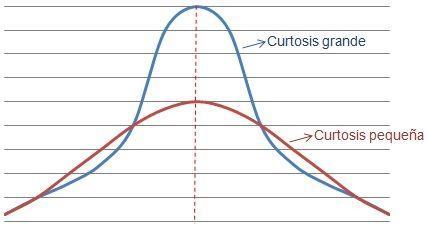
La curtosis (o apuntamiento) es una medida de forma que mide cuán escarpada o achatada está una curva o distribución.

Este coeficiente indica la cantidad de datos que hay cercanos a la media, de manera que a mayor grado de curtosis, más escarpada (o apuntada) será la forma de la curva.

La curtosis se mide promediando la cuarta potencia de la diferencia entre cada elemento del conjunto y la media, dividido entre la desviación típica elevado también a la cuarta potencia. Sea el conjunto X=(x1, x2,…, xN), entonces el coeficiente de curtosis será:

En la fórmula se resta 3 porque es la curtosis de una distribución Normal. Entonces la curtosis valdrá 0 para la Normal, tomándose a ésta como referencia. Cuando los datos están agrupados o agrupados en intervalos, la fórmula del coeficiente de curtosis se convierte en: