MODA

Por Katherin

En muchos ámbitos de la ciencia y en algunos trabajos en que se ocupa la estadística necesitamos de muchas técnicas o medidas de posición que ayudan a conocer un dato que nos interesa, una de estas medidas son los percentiles llamadas medias de posición no central (cuartiles, deciles, quintiles, percentiles) que se puede describir como una forma de comparación de resultados.

A continuación, se presenta algunos aspectos que son considerados importante dentro de las medidas de posición (percentiles) son:

Chuquilla

 Es una medida de posición.: Indica, una vez ordenados los datos de menor a mayor, el valor de la variable por debajo del cual se encuentra un porcentaje dado de observaciones en un grupo.  Divide la muestra de datos en 100

partes o grupos

 Ordena los datos de menos a mayor por lo que funciona bien en datos cuantitativos

El percentil, en estadística, es un valor que sirve para comparar un conjunto ordenado de datos, en otras palabras, el percentil nos indica en el caso de los bebés y niños si, comparados con otros de su misma edad y sexo, se encuentran dentro de la media.

El primer ejemplo que se presenta es muy común para aquellas personas que tienen hijos, hermanos, sobrinos y que han tenido la oportunidad de acompañar a sus padres a llevarlos a las consultas pediátricas fíjense ustedes que cada vez que llevamos a un niño recién nación el medico esta pendiente de la talla, el peso, el diámetro del cráneo y lo chequean en fusión de la edad, hay un conjunto de tablas que cada país construye que permite comparar la talla y el peso en función de la edad nos permite compararlos con otros niños las mismas condiciones.

Con ayuda del ejemplo ya antes mencionado, se observará lo sencillo que es interpretar los percentiles: Cuando el pediatra nos dice que el niño está en el percentil 25 de altura, significa que, de cada 100 niños de su edad, 75 son más altos que nuestro hijo y 24 serían más bajos

Otro claro, ejemplo también se puede manifestar los resultados se interpretan como percentiles de promedio. Por ejemplo, si un bebé tiene una estatura en el percentil 75, significa que alrededor del 25% de los niños de la misma edad y sexo son más altos y alrededor del 75% son más bajos en estatura.

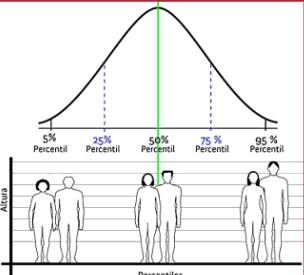
Finalmente, los percentiles son muy útiles en distintas maneras de usarlo sirve para comparar un conjunto ordenado de datos, como puede ser el peso y la talla de un niño con el resto de niños de su edad en un momento concreto. De esta forma podríamos decir “este niño está en la media de peso para su edad” o “es de los que más pesa de su clase”, o también “es de los más altos de su clase” o “de los más bajitos”, dependiendo de si su percentil de peso o talla es alto o bajo.