Power system analysis and design 6th edition glover solutions manual by naomi.thomas570

Visit to download the full and correct content document: https://testbankdeal.com/dow nload/power-system-analysis-and-design-6th-edition-glover-solutions-manual/

Power System Analysis and Design 6th Edition Glover Solutions Manual

Chapter 8 Symmetrical Components

ANSWERS TO MULTIPLE-CHOICE TYPE QUESTIONS

8.1 ±±°Equal,120°; equal,120; equal, zero

8.2 120 13 1; 22 j ej ° −+

8.3 ++++ ++

8.21 3 gon ZZ +

8.22 Positive-sequence, sub-transient 8.23 Does not

8.24 a

2 012012 2 012

;; VVVVaVav VaVaV

8.25 (i) Can, do; does not, 3 (ii) 3030:1,:1jjee °−° (iii) Donot

2 2

11 33;; 1 3

VVVVaVaV VaVaV

8.4 () () () ++++ ++

abcabc abc

8.5 Zero

8.6 May, Never

8.7 a

8.8 0 ;3 abc IIII ++

8.9 Zero

8.10 a

8.11 a

8.12 a

8.13 ; Ynn ZZZ +

8.14 1 p AZA

8.15 a

8.16 3 YnZZ +

8.17 ∆∆ ∞,/3,/3 ZZ

8.18 Diagonal, uncoupled

8.19 Uncoupled, positive-sequence

8.20 Diagonal, zero

8.26 (i) Short (ii) 3 n Z (iii) Open (iv) Short

8.27 3

8.28 *** 001122 ++ VIVIVI

(d)

8.3 (a)

(b)

I Iaa Iaa

 ∠°∠°+∠°+∠°    ∠°∠°+∠°+∠° =   =   ∠°∠°+∠°+∠°  

3 1622019012001340

00.28560.57190

−∠−°   +=∠°  =

602.975.9490A

3 00.3160.63290

 +∠° 

j j j

11140901901018.8645

 ∠°∠°+∠°∠°    ∠°∠°+∠°=∠°  ==   ∠°+∠°∠°  

1140040190112025.76105A

8.4 2 2

111458018020190

 ∠°∠°+∠°+∠°    =∠°=∠°+∠°+∠°     ∠°∠°+∠°+∠°  

V Vaa Vaa

an bn cn

19004518022401210

1459018021201330

200 © 2017 Cengage Learning®. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 8.1 UsingtheidentitiesshowninTable8.1 (a) () 222 1(1)(1)3303 90 112(1)22402 aa aaaaa −−−−∠−° ===∠° +−++−−∠° (b) ( ) () () 2 2 12135 13 1120 22 215215 0.7321270 1.932105 13 1 22 aaj j jaaaja jj j −+ −+∠° == ++  ∠°−+   ∠°∠° ===∠° ∠°  −++   (c) ( )( ) ( )( ) 223 1110 aaaaa ++=−−==∠° (d) ( )( ) ( )( ) ( )( ) 22221132703303300aaaaaa −−=−−=∠°∠°=∠° 8.2 (a) () ()3 10 3 13 22aaaaj ===−+ (b) ()()()()()()() 101010442 13 22jajajjjaaj ===−=−

3 1330390033 05.196 aj j −=∠−°=∠−°=− =−

−+− ==∠ =∠°=+ 131 222 3 radians 2 0.606549.620.39290.4620 j a eee j

0 2 1 2 2

11169019013201220

1163201901801100

2 1 2 2

Iaa

1019012406.90165 I Iaa

2.1741.985132.4842.4

+∠°   =−−=∠°   +∠° 

451.6921.24794.58216.4

0.03972.21799.7888.97

j jV j

8.5 Eq. (8.1.12) of text:

()

abc IIII j

0 1 3 1 10089061501.601281.6672.3146.15A 3

=++ =∠°+∠−°+∠°=−=∠−°←

()

abc IIaIaI j

2 1 1 3 1 100112089012406150

()() ( )

=++ =∠°+∠°∠−°+∠°∠° =∠°+∠°+∠°=+=∠°←

()

3 1 1008306307.372.337.7417.56A 3

2 2 1 3 1 100124089011206150

=++

abc IIaIaI j

=∠°+∠°∠−°+∠°∠°

() ()() ( ) ()

3 1 10081506901.020.6671.2233.07 3

=∠°+∠°+∠−°=−=∠−°←

8.6 (a)Eq. (8.1.9) of text:

( )

10080304030114201169.9V a VVVV j =++ =∠°+∠°+∠−°=+=∠°←

() 012

=++

2 012

b VVaVaV j

1001240803011204030

()()

  =∠°+∠°∠°+∠°∠−°   =∠°+∠−°+∠°=−=∠−°←

()

10080904090104041.376

=++

2 012

c VVaVaV j

1001120803012404030

()()

  =∠°+∠°∠°+∠°∠−°   =∠°+∠°+∠−°=−+=∠°←

()

1008015040150942096.1168

201

2017 Cengage Learning®. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.

(b) ( ) ( )

1142010401046012030V abab VVVjjj =−=+−−=+=∠°←

( ) ( )

104094201046012030V bcbc VVVjjj =−=−−−+=−=∠−°←

( ) ( ) 9420114202080208180V caca VVVjjj =−=−+−+=−+=∠°←

() () () 0

11 12030120302081800 33ababbcca VVVV=++=∠°+∠−°+∠°=←

2 1

11 331240208180

12030112012030

() () ( ) () ()

ababbcca VVaVaV j

 ∠°+∠°∠−° =++=  +∠°∠°   =∠°+∠°+∠°=+=∠°←

1 12030120902086069.33120138.660V 3

() () ()

2 2

12030124012030 11 331120208180

ababbcca VVaVaV j

 ∠°+∠°∠−° =++=  +∠°∠°  

( ) () ()

1 120301202102086034.676069.360V 3

=∠°+∠°+∠−°=−=∠−°←

Since ( ) 00 0 0 abab VVV=−=

And ( ) ( ) 121122 ; abababab VVVVVV =−=− , we have ( ) ( )°° 01122 0;330;330LLLLLL VVVVV ==∠=∠−

Or 11 1 30 3 LVV  =∠−°   and 22 1 30 3 LVV =∠°  

Applyingthe above, one gets

()

1 1 30138.660803069.340 3 V j  =∠−°∠°=∠°=+←  

()

2 1 3069.360403034.620 3 V j  =∠°∠−°=∠−°=−←  

Phase voltages are then given by 12 103.920105.910.9V a VVVj=+=+=∠°←

2 12 1240803011204030

b VaVaV j =+=∠°∠°+∠°∠−° =∠−°+∠°=−=∠−°←

( ) ( )

()

80904090404090V

2 12 1120803012404030

( ) ( )

c VaVaV j =+=∠°∠°+∠°∠−° =∠°+∠°=−+=∠°←

801504021010420105.9169V

The above are not the same as inpart (a) ←

However, either set will result inthe same line voltages. Note that the zero-sequence line voltage is always zero,even though zero-sequence phase voltage mayexist. Soit is not possible toconstruct the complete set of symmetrical components of phase voltages even whenthe unbalancedsystemof line voltages is known. But we can obtain a set with no zero-sequence voltage torepresent the unbalanced system.

2017 Cengage Learning®. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.

202 ©

8.7

Current to ground, 0 3100090 n IIA ==∠°

8.8 ;; ababbcbccaca VVVVVVVVV =−=−=−

0 2 1 2 2 11101150130 1 1200 1120015012701270 3 3 11200301301150 40090 800270

I Iaa Iaa A  ∠°+∠°    ∠°∠°+∠° =

    ∠°∠°+∠°   ∠°   =∠°   ∠° 

40090

000

abV

reference, () () () () () () () () () ()() () 2 1 2 22 222 222 1 30 1 1 3 1 3 1 3 1 3 1 11 3 3 ababbcca abbcca abcabc abcabc abca j a VVaVaV VVaVVaVV VaVaVaVVaV VaVaVaVaVaV aVaVaVaV Ve

=++−++   =++−++   =−++=−  =← () () () () () () () () () ()() () 2 2 2 2 2 22 2 2 30 2 1 3 1 3 1 3 1 3 1 11 3 3 ababbcca abbcca abcabc abcabc abca j a VVaVaV VVaVVaVV VaVaVaVVaV VaVaVaVaVaV aVaVaVaV Ve−° =++ =−+−+− =++−++  =++−++   =−++=−  =←

0,0abbccaabbcca VVVVVV++==== ∵ Choosing

as the

° =++ =−+−+−

8.9 Choosing bcV as reference andfollowingsimilar steps as in Problem8.8 solution, one can get

∠°

  ∠−° =     ∠° 

 

28002501102901302.6964.257

∠°+∠−°+∠°−   =∠°+∠°+∠°=+ 

1 28002501029010270.631.26 3 28002501302902506.70627

 ∠°+∠°+∠°− 

5.03957.65

∠−°  =∠°   ∠−° 

272.46.59V

27.8276.05

j j j

(b)2800250110

abagbg

−∠°−∠−°   ==∠−°−∠°    ∠°−∠°  

VVV V VV V VV

bc bgcg

ca cgag

250110290130

2901302800

+∠°   =−=∠−°   −+∠° 





∠°+∠−°+∠°+    =∠°+∠°+∠°=+    ∠°+∠°∠+∠°−−  

     =∠+°      ∠−° 

1 2

90 0111 90 222 0;33; and 33 j bcbcaa j bcaa VVVejV VVejV −° °  ===−  ←  ==  

0 2 1 2 2 1112800 11250110 31290130 Lg Lg Lg V aa V aa V

8.10 (a)



100.9457.1468.177.55V 466.4222.2516.6154.5



365.5234.9434.532.73

j j j 434.532.73468.177.55516.6154.500 1 434.532.73468.142.55516.634.5378.9281.2 3 434.532.73468.1162.5516.6274.513.4646.44 0 471.836.58 48.35106.2

∠°    ∠−° =     ∠° 

j j j

330 330 Lg Lg

  =∠°   ∠−° 

8.11 The circuit is shown below:

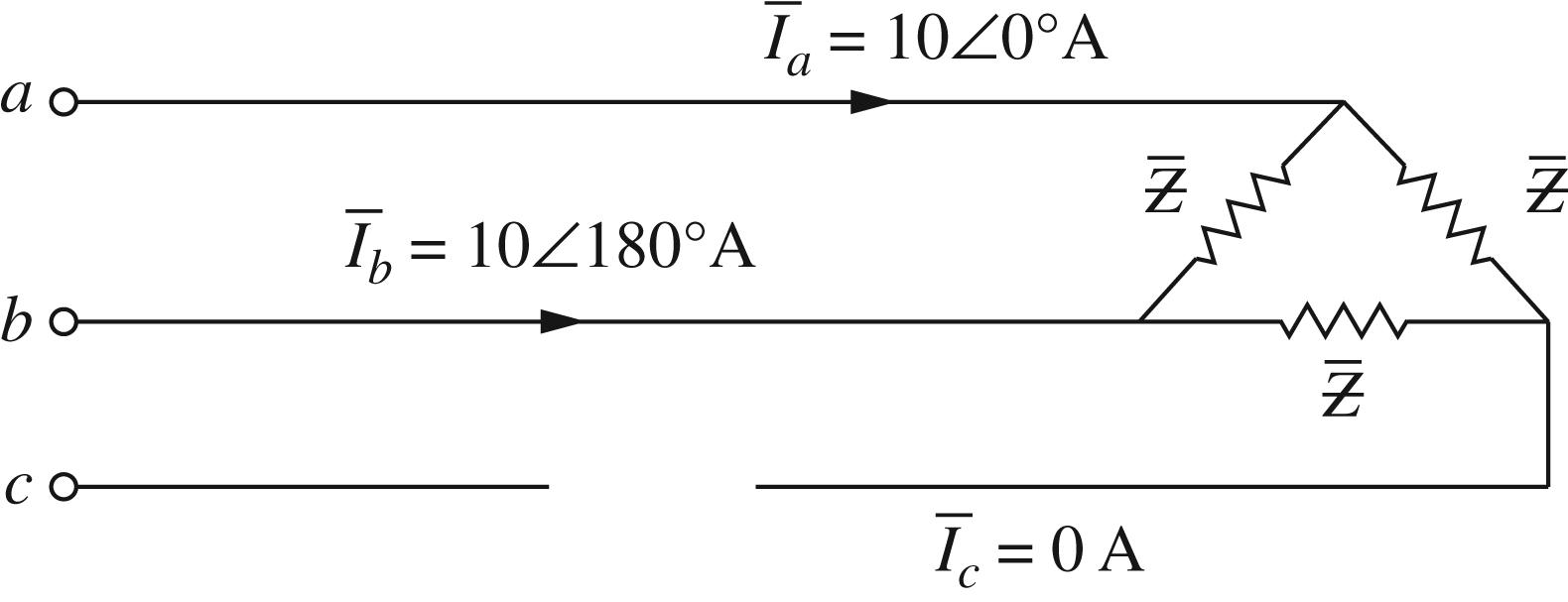
1 1001018000

I I j I j

a a a

0 1 2

=∠°+∠°+= =∠°+∠°+°+=−=∠−° =∠°+∠°+°+=+=∠°

3 1 10010180120052.895.7830A

3 1 10010180240052.895.7830A

Then 00 00

IIII IaIIaI IaIIaI

ba ca baca ba ca

2 1111 2 22 22

==== ==∠−°==∠° ==∠°==∠−°

0A;0A 5.78150A;5.7890A 5.78150A;5.7890A

8.12 Selecting a base of 2300 V and 500 kVA, each resistor has an impedance of10pu ∠° ; 0.8 abV = ;1.2 bcV = ;1.0 ca V =

The symmetrical components of the line voltages are:

abV j =∠°+∠°−°+∠°+°=+

( ) 1 1 0.882.81.212041.41.02401800.27920.9453

0.985773.6

abV j =∠°+∠°−°+∠°+°=−−

( ) 2 1 0.882.81.224041.41.01201800.17900.1517

(These are in pu on line-to-line voltage base.)

0.2346220.3

Phase voltages in pu on the base of voltage to neutral are given by

0.985773.6300.985743.6

V V =∠°−°=∠° =∠°+°=∠° [Note: An angle of 180° is assigned to ca V ]

an an

0.2346220.3300.2346250.3

Zero-sequence currents are not present due to the absence of a neutral connection.

IV IV =∠°=∠° =∠°=∠°

aa aa

11 22

/100.985743.6pu /100.2346250.3pu

The positive direction of current is from the supply toward the load.

() () ()

=∠°

8.13 (a)

∠° 

111100 111290

 ∠−° = 



I Iaa Iaa

 ∠° 

100129015903.33313.4816.7

∠°+∠−°+∠°+∠°   =∠°+∠°+∠°=−=∠−°   ∠°+∠°+∠°−−∠−° 

10012301533011.130.511.142.58

10012150152104.460.54.49173.6

j jA j

(b)1001590101518.0356.3

−∠°−∠°−∠−° 

 

1290100101215.62129.81

=−=∠−°−∠°=−−=∠−°    −∠°−∠−°∠° 

IIIj IIIjA IIIj

aabca bbcab ccabc



15901290272790

11118.0356.3

0 2 1 2 2

18.0356.315.62129.812790

∠−°+∠−°+∠°     =∠−°+∠−°+∠°    ∠−°+∠−°+∠°  

  ∠°   1

1 18.0356.315.629.8127330 3 18.0356.315.62249.8127210 0000

16.2610.3919.2932.573 6.2574.617.77143.59

j jAI j ∆

+   =−=∠−°=∠   −−∠−°  2

  −°   ∠+° 

30 330 I∆

0 0 0 1 1 1 2 2 2 5.03957.65 0.252110.78 2053.13 272.46.59 13.6246.54 2053.13 27.8276.05 1.391129.18 2053.13 Lg Lg Lg V I A Z V I A Z V I A Z ∠−° ===∠−° ∠° ∠° ===∠−° ∠° ∠−° ===∠−° ∠°

206

2017 Cengage Learning®. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.

0 2 1 2 2

311590 ∆ ∆ ∆

1115.62129.81 312790

(c)

L L L I Iaa Iaa

 ∠−°    ∠−° =  

8.14

8.15

 ∠−° 

I Iaa Iaa

1110.252110.78 113.6246.54

  =∠−°

 

11.391129.18

  ∠−°  

a b c

0.2520110.7813.6246.541.391129.18

∠−°+∠−°+∠−° =∠−°+∠°+∠−°

0.2520110.7813.62193.461.3919.18

        °+∠°  

0.2520110.7813.6273

∠−°+∠ .461.391110.82

−∠−° 

8.411.21453.13

11.963.62812.5163.1

 =−−=∠−° 

3.29414.1214.576.37

 +∠° 

j jA j

Note: The source and load neutrals are connected with a zero-ohm wire.

Vz I IVz I Vz

  ∠°∠°∠−°     ==∠−°∠°=∠−°       ∠°∠°∠°    

agY a bbgY c cgY

28002053.131453.13

2501102053.1312.5163.1

2901302053.1314.576.87

Which agrees with the above result.

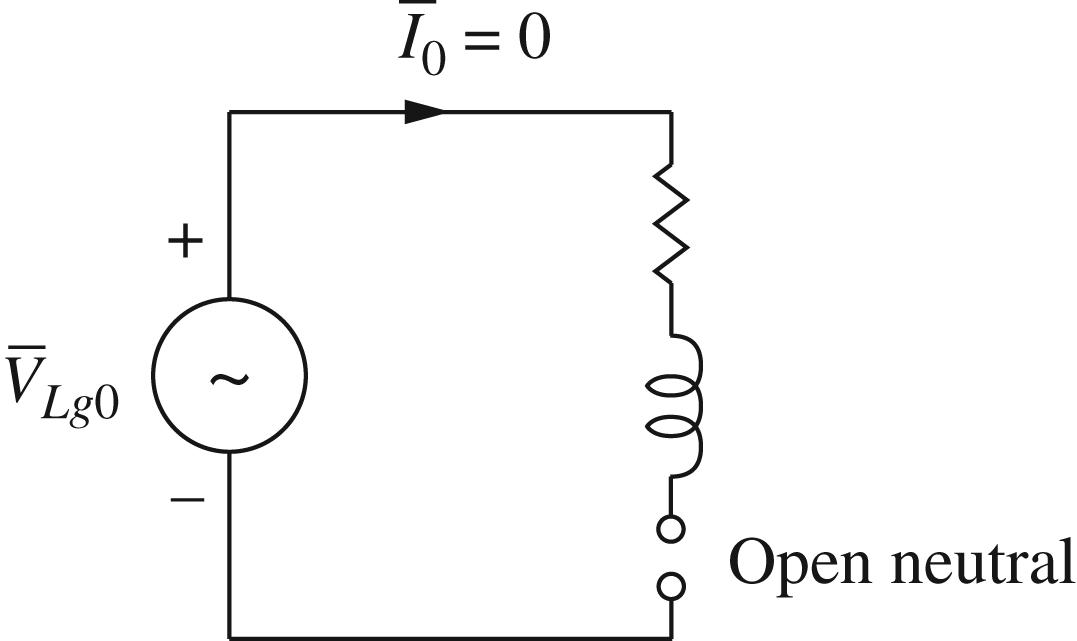
0 0 I = ; From Problem 8.14, 1213.6246.54A;1.391129.18AII =∠−°=∠−°

    =∠−°  

b c

  ∠−°  

13.6246.541.391129.18 13.62193.461.3919.18

∠−°+∠−°   =∠°+∠−° 

I Iaa Iaa j j j

13.6273.461.391110.82

 ∠°+∠° 

8.4910.96

∠−°   =∠° 

=−− +

11.873.392

3.3831

4.3614.7576.74

 ∠° 

2 2

2 2 1110 113.6246.54 11.391129.18

13.8652.24 12.35195.9A

Note: These currents are 3 times those in Problem 8.15.

 ∠−° 

  =∠−°  

I Iaa Iaa

a b c

  ∠−°  

∠−°+∠−°+∠−° =∠−°+∠°+∠°

   

 

∠−°+∠°+ 137.28

  ∠°  

33.216.4937.0726.41

−∠−° 

 =−−=∠° 

24.7422.7533.61222.6A

9.41638.1539.29103.9

j j j

 −+∠° 

208 © 2017 Cengage Learning®. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 8.16 01 2 2 2 272.46.59 0;40.8646.54A 20 53.13 3 27.8276.05 4.173129.18A 20 53.13 3 111041.5852.24 140.8646.5437.05195.9 14.173129.18 a b c II I I Iaa Iaa ∠° ===∠−°  ∠°   ∠−° ==∠−°  ∠°    ∠−°    =∠−°=∠°     ∠−°   A 44.2576.74     ∠° 

8.17 0 0 0 1 1 1 2 2 2 5.03957.65 0.4826131A 310 272.46.59 36.5419.98A 7.45426.57 27.8276.05 3.732102.72A 7.45426.57 Lg Lg Lg V I Zj V I Z V I Z ∠−° ===∠−° + ∠° ===∠−° ∠°

===∠−° ∠° 2 2 1110.4826131 136.5419.98 13.732102.72

0.482613136.54220.023.73217.28 0.482613136.54100.023.732

∠−°

0.482613136.5419.983.732102.72

8.19

209 © 2017 Cengage Learning®. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 8.18 00102 2 10112 2 20212 111 11 31 ZZZ ZZZaa ZZZaa    =    ( )( )( ) ()()() ()()() 2 2 2 2 2 2 aaabacaaabacaaabac abbbbcabbbbcabbbbc acbcccacbcccacbccc ZZZZaZaZZaZaZ ZZZZaZaZZaZaZ ZZZZaZaZZaZaZ   ++++++   ++++++     ++++++   ( ) ( ) () () () () () () () () () () () () () () () () () 2 22 222 22 2 332224 42 2 1 11 3 11 11 aabbccabacbc aabbccabacbc aabbccabacbc aabbccabacbc aabbccabacbc aabbcc ZZZZZZ ZaZaZZaZaZaa ZaZaZZaZaZaa ZaZaZZaZaZaa ZaZaZZaaZaaZaa ZaZaZZ  +++++  =++++++++   ++++++++  ++++++++ ++++++++ +++ () () ( ) () () () () () () () () () () () ( ) 2224 2 22 24 2 33222 2 11 222 abacbc aabbccabacbc aabbccabacbc aabbccabacbc aaZaZaa ZaZaZZaZaZaa ZaZaZZaZaZ ZaZaZZaaZaaZaa ++++  ++++++++  +++++   ++++++++  22 22 22 22 22 222 1 3 222 aabbccabacbc aabbccabacbc aabbccabacbc aabbccabacbc aabbccabacbc aabbccabacbc aabbccaba ZZZZZZ ZaZaZaZaZZ ZaZaZaZaZZ ZaZaZaZaZZ ZZZZZZ ZaZaZaZaZZ ZaZaZaZaZ +++++   =++−−−   ++−−−  ++−−− ++−−− +++++ ++−− 2 2 222 cbc aabbccabacbc aabbccabacbc Z ZaZaZaZaZZ ZZZZZZ   +++++   ++−−− 

(a)

writing KVL equations [see Eqs (8.2.1) – (8.2.3)]:

In matrix format [see Eq (8.2.4)]

 +  

  +=     

   + 

  +∠°  

+=∠°  

  +∠°  

 +∠°

  =+∠° 

Performing the indicated matrix inverse (a computer solution is suggested):

 ∠−°∠°∠°∠°  

0.176356.500.02618150.20.02618150.21000

   =∠°∠−°∠°∠°

  

I I I



a b c

  ∠°∠°∠−°∠°  

Finally, performing the indicated matrix multiplication:

17.6356.501.964330.21.309240.2

 ∠−°+∠°+∠°  

   =∠°+∠°+∠°

2.618150.213.22123.51.309240.2

  

   ∠°+∠°+∠°   

 

2.618150.21.964330.28.81533.5

10.7816.81

  =−+

 

I I I Ij Ij Ij

a b c a b c

10.2211.19

  +  

6.7835.191

∠−°   =∠°   ∠° 

19.9757.32 15.15132.4A 8.54137.43

( ) () () agyanabc bgybnabc cgycnabc VZIZIII VZIZIII VZIZIII =+++ =+++ =+++

( ) () () ynnn

nynnbbg c

nnyn ZZZZ

ZZZZIV I V ZZZZ

ag a

V I



 () () () () () () 11 11 11 1 11 11 11 351000 3575180 355090 351000 3575180 355090 a b c a b c jjjI jjjI jjjI Ijjj Ijjj Ijjj

 

  

+∠°   



0.02618150.20.176356.500.02618150.275180

0.02618150.20.02618150.20.176356.505090

(b) Step (1): Calculate the sequence components of the applied voltage:

 ==∠°     ∠°   

∠°+∠°+∠° 

 =∠°+∠°+∠°   ∠°+∠°+∠°  +   =−  + 

8.33316.667 60.2729.98

∠°  =∠−   ∠° 

18.6363.43 67.3226.45V 34.1122.99

Step (2): Draw sequence networks:

Step (3): Solve sequence networks

18.6363.4318.6363.43 3377.61666.80

2.4463.37A

∠−°∠−° ====∠− +∠°

∠° ===∠−° ∠°

Step(4):Calculatethelinecurrents(phasecomponents):

1112.4463.37

 ∠−°    =∠−°

I Iaa Iaa

a b c

113.4679.58 16.82230.14

 

  ∠−°  

2.4463.3713.4679.586.82230.14

∠−°+∠−°+∠−° =∠−°+∠°+∠°

2.4463.3713.46160.426.82289.86

        °  

2.4463.3713.4640.426.82220

∠−°+∠°+∠ 9.86

10.7816.8119.9757.32

−∠−°   =−+=∠°   +∠° 

10.2211.1915.15132.4A

6.7735.1878.53137.45

j j j

0 2 1 2 2 1111000 1 175180 3 15090 1000751805090 1 10007530050330 3 1000756050210

31.4013.32 g g g V Vaa aa V

j  ∠°  

00 1 0 0 0 1 1 2 2 2

34553.13

6.82230.14

gg yn g g

I V

Zj V

====

67.3226.4567.3226.45 13.4679.58A

34.1122.99

553.13

VV I ZZZj

∠°∠°

++∠° =∠−°

2 2

8.20

Transformingtosymmetricalcomponents,

Premultiplying each

As shown in Fig. 8.5 of the text, sequence networks for an equivalent Y representation of a balanced-∆ load are given below:

(b)With a mutual impedance of



between phases,

  =  

    

Rewriting the coefficient matrix into two parts,



jjj jjjjj jjj

2766100111

6276210106111

 =+   

6627001111

∆ currentsby 2700 0270 0027 ab ab bc bc ca ca VjI VjI VjI     =      

(a) Theline-to-linevoltagesarerelatedtothe

0 0 1 1 2 2 2700 0270 0027 ab ab ab ab ab ab VI j AVjAI j VI     =       

side by 1 A , 00 0 1 11 1 22 2 2700 270270 0027 abab ab abab ab abab ab VII j VjAAIjI j VII     ==       

Ω

0 0 1 1 2 2 2766 6276 6627 ab ab ab ab ab ab VI jjj AVjjjAI jjj VI 

(j6)