APRENDER HACIENDO MATEMÁTICA

APRENDER HACIENDO MATEMÁTICA


Libro de MATEMÁTICA para segundo grado de la educación primaria




Libro de MATEMÁTICA para segundo grado de la educación primaria
Profesoras de Matemática de la Universidad Nacional de Rosario
Noemí Buschiazzo de González Beltrán
Susana Filipputti de García
Liliana Lagreca de Cattaneo
Noemí Lagreca de de la Pace
Susana Strazziuso de Hinrichsen
P roblemas y
R azonamiento en la
E nseñanza de la
M atemática
3 (para tercer grado)
Datos relativos a la edición: Et ulligent etur as del ilia dignist et as que pelenim il inte eossit eosantibus nest liquaturio dolo maioris quiam ilias sam quia dissimp erspitae doluptasiti quos que nossunti odipis apis dolenisi nonecto tatur? Pidignihicil Etur? Iquia si senihiciat et ma poritibus si dolorem eum et ab idem a nulla idit aciendi odicips apelit od ma dolupta perum facias modi cus, sit alit quam aut et ut omnis molorpos volorest.
Dedicamos este libro a nuestros alumnos y exalumnos con quienes hemos trabajado esta maravillosa ciencia, la “Matemática”. Las autoras
PREM 3 es un libro para tercer grado de la educación primaria que enseña Matemática haciendo Matemática.
¿Cómo está organizado el libro?
Está organizado en base a colecciones de problemas que se agrupan atendiendo a los distintos campos conceptuales:
• Números y operaciones, en sus diversos lenguajes
• Geometría
• Mediciones
• Estadística y Probabilidad
Estos problemas responden al desarrollo de todos los contenidos que, para cada uno de los campos, proponen los diseños curriculares actuales. Se han considerado en su selección, los aspectos que sobre el tratamiento de los mismos sugieren los documentos oficiales, como así también las orientaciones que, durante los últimos años, se han postulado a través del Instituto IREM (Instituto de Investigación de la Enseñanza Matemática) radicado en Francia, para la Didáctica de la Matemática.
De esa forma, mediante la propuesta de problemas, se organiza el aprendizaje constructivo de los conceptos y de los algoritmos, el reconocimiento y construcción de figuras, el reconocimiento y aprendizaje de los procesos de medición, la interpretación de gráficos, entre otros aspectos. Los contenidos son abordados desde la estructura lógica de la Matemática y en el marco de la secuenciación que el tratamiento del área supone.
Esta organización, además, atiende a la interrelación que debe plantearse entre los contenidos de los diversos campos conceptuales y a la contextualización que debe caracterizar a la propuesta de los temas, en la Matemática de hoy.
Los problemas de cada campo conceptual presentan dificultades crecientes, profundizando saberes abordados anteriormente. Se retrabajan los contenidos conceptuales y se guía el proceso para descubrir regularidades y algoritmos de cálculos diversos.
Algunos problemas tienen como meta el iniciar a los alumnos en el manejo inteligente de la calculadora, entendida como un instrumento de trabajo, que didácticamente tiene una riqueza tan grande como su capacidad operatoria.
Es importante señalar que los distintos campos pueden abordarse simultáneamente, asegurando así la posibilidad de que un mismo contenido sea trabajado desde distintos puntos de vista.
Por ello, al comenzar el tratamiento de los diversos campos conceptuales, se proponen problemas simples, posibilitando el inicio simultáneo de los mismos integradamente, dando de esta forma funcionalidad a los contenidos. Así, al trabajar el proceso de medición de cada magnitud, en el campo de las Mediciones se han considerado al principio, problemas donde la unidad elegida “entra” un número entero de veces en el objeto a medir, vinculando los temas trabajados con el abordaje de los números naturales Posteriormente, en concordancia, con el tratamiento de “las fracciones”, se introduce la idea de que la unidad “no cabe un número entero” de veces en el objeto a medir, siendo necesario la creación de fracciones de la unidad de medida. Idéntico procedimiento se ha empleado al abordar el campo de la Estadística y la Probabilidad proponiendo problemas sobre el particular, en el desarrollo de los campos conceptuales, favoreciendo la integración del área.
En el trabajo sobre la Geometría se proponen problemas que atienden fundamentalmente al desarrollo del pensamiento intuitivo permitiendo visualización y la reproducción de figuras a través del uso de distintos materiales como geoplanos, papeles punteados, entre otros.
Nuestro propósito es “proponer problemas” que el alumno resuelva por sí mismo, sin recurrir a la tutela permanente del docente. Es decir, tender al trabajo autónomo de los niños.
Al finalizar la propuesta de problemas, en cada campo, se proponen actividades de autoevaluación, en algunos casos bajo la forma de “elección múltiple” que permitirán una evaluación de los contenidos tratados. Además se encontrarán, al final del libro, cuatro fichas, hojas de papel punteado y una hoja de calcos que constituyen un material para resolver los problemas de un modo más dinámico.
En esta nueva edición del Matemática 3 hemos tratado de introducir y trabajar las nuevas tendencias, en lo que respecta a estrategias de cálculo, escritas, mentales y mecánicas. Por esta razón, pueden resultar propuestas no triviales, que suponen la no mecanización y tienden al desarrollo del pensamiento lógico, sin descartar el pensamiento intuitivo de los alumnos de este nivel. Estas propuestas no triviales resultan novedosas, dando ellas lugar a un proceso continuo de adecuación a nuevas formas de trabajar, operar y pensar.
Como siempre, hacemos nuestro el lema:
“MATEMÁTICA SE APRENDE, HACIENDO MATEMÁTICA”

Hacé como Sulino y pegá la etiqueta con tu nombre y apellido. La podes encontrar en la página de CALCOS 0 (pág.*)
¡AHORA SÍ! YA SABEMOS DE QUIEN ES CADA LIBRO

Yo soy SULINO
Este año vamos a seguir aprendiendo matemática juntos.
¡Manos a la obra!
CAPÍTULO
• Lectura, escritura y formación de números de hasta tres dígitos
• Relación de orden
• Operaciones y relaciones inversas: suma y resta, multiplicación y división
• Recolección, información e interpretación de datos
• Actividades de autoevaluación
• Los números de cuatro dígitos: obtención, lectura, escritura y composición
• Operaciones y relaciones inversas.
• Extensión del uso de algoritmos de cálculo
• Los números y la organización de la información
• Actividades de autoevaluación
• El concepto de fracción
• Datos significativos de las fracciones
• Comparación de fracciones
• Fracciones equivalentes
• Las fracciones usadas para expresar “probabilidades”
• Actividades de autoevaluación
CAPÍTULO 4
• Ubicaciones y posiciones: derecha, izquierda, abajo, arriba, puntos cardinales
• Recorridos: lectura de planos y mapas elementales, caminos, direcciones, giros, construcción y reconocimiento
• Las formas geométricas del espacio (poliedros y cuerpos redondos) y del plano (rectas, ángulos, polígonos, círculos)
• Reconocimiento, descubrimiento de regularidades, reproducción
• Actividades de autoevaluación
CAPÍTULO 5
• La medición de distintas magnitudes: el dinero, la longitud, la capacidad, el tiempo y el peso
• El proceso de medición: la determinación de la medida.
• Unidades convencionales y no convencionales
• Relación entre las mediciones y los números enteros y/o fraccionarios
• Actividades de autoevaluación
CAPÍTULO 6
• Recopilación de datos, organización e interpretación
• Actividades de autoevaluación


CAPÍTULO 2
Carlos, Ale y Nacho se van de viaje a córdoba y cada uno se lleva sus ahorros.

¿Cuánto tiene ahorrado? Tiene $

¿Cuánto tiene ahorrado? Tiene $

Carlos Ale Nacho
¿Cuánto tiene ahorrado? Tiene $
El papá de los 3 hermanos decide darle algo más a cada uno.

A Carlos le da: A Nacho le da: A Ale le da:
¿Cuántos billetes de cien tiene ahora?
¿Cuánto dinero tiene? 900 +
¿Cuántos billetes de diez tiene ahora?
¿Cuánto dinero tiene? 990 +
¿Cuántos monedas de $1 tiene ahora?
¿Cuánto dinero tiene? 999 +


Los chicos quieren saber cuánto tienen, Carlos lo hizo de esta manera:
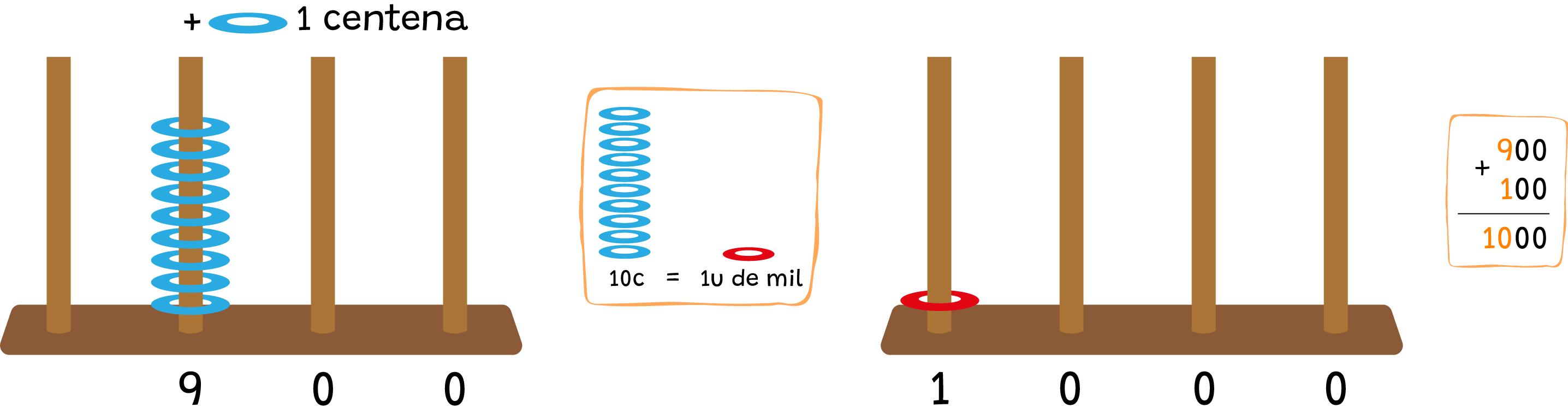
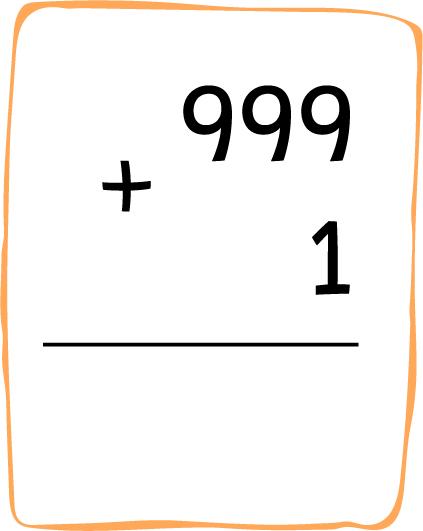
Ayudá a Ale y Nacho a completar sus cuentas.
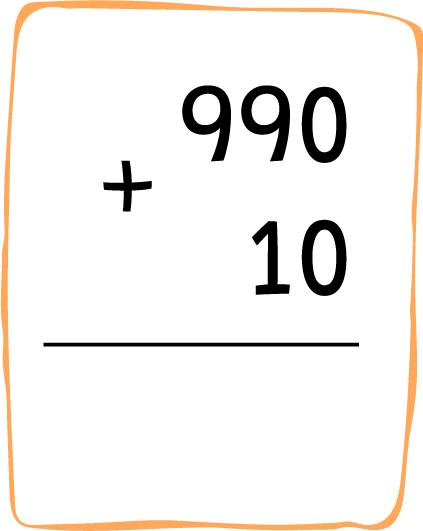
Ale: Nacho:
Entonces:

¿Con cuántos billetes de $100 se reúnen $1000?
¿Cuántos cienes hay en mil? cienes
¿Con cuántos billetes de $10 se reúnen $1000?
¿Cuántos dieces hay en mil? dieces
¿Con cuántas monedas de $1 se reúnen $1000?
¿Cuántos unos hay en mil? unos

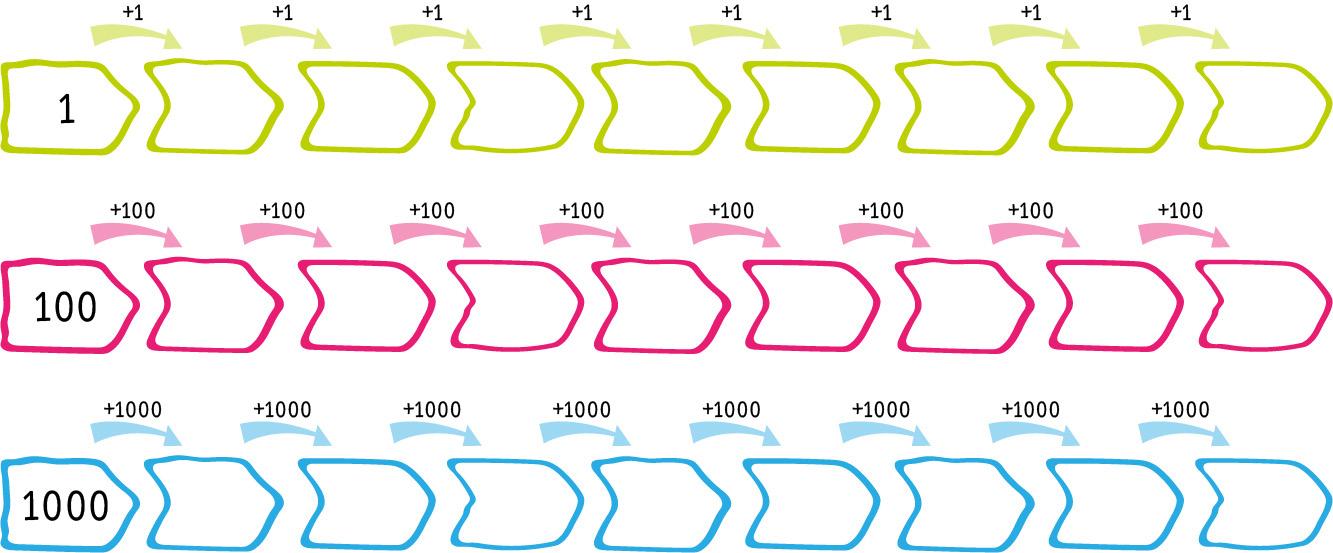
Completá las escalas
¿Cuántas veces sumaste 100?
¿Es mil un número par? ¿Por qué?
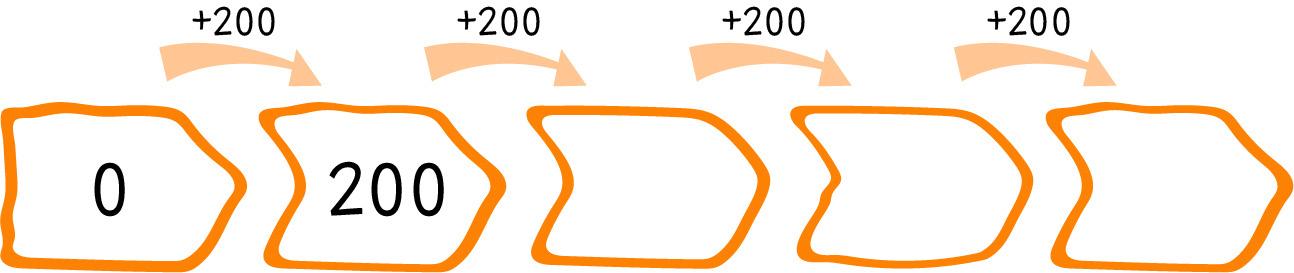
¿Cuántas veces sumaste 200?
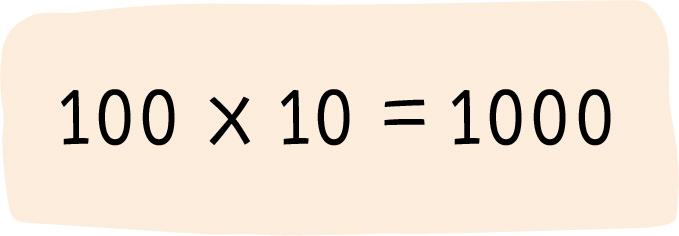


Completá con MÁS o MENOS
A tu escuela concurren de 1000 alumnos.
En el estadio de fútbol más grande de mi ciudad entran de 1000 personas.
Un kilogramo de nueces tiene de 1000 nueces.
La biblioteca de tu escuela tiene de 1000 libros.
Lola está entretenida con un juego que tiene en la computadora. Cada vez que gana, suma una unidad de mil más. Ya tiene 1000 puntos, es decir, 1u de mil.
Completá el cuadro para ver cuantos puntos juntó en el día
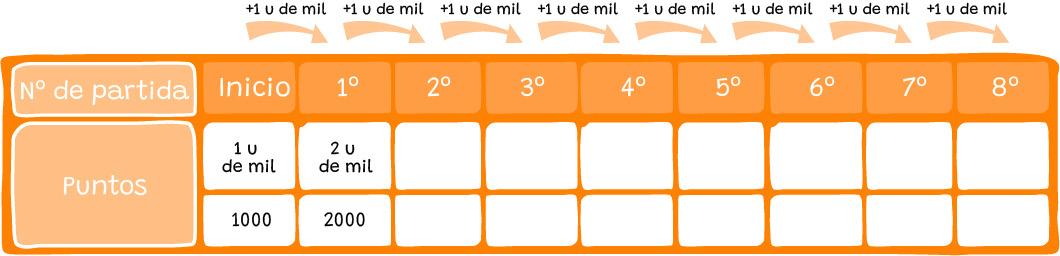
Leé y completá
Si en el visor de tu calculadora figura el doscientos, ¿cómo lo transformarías en 1000 con una sola cuenta? Escribila

Si en el visor de tu calculadora figura el quinientos, ¿cómo lo transformarías en 2000 con una sola cuenta? Escribila
Si en el visor de tu calculadora figura el ciento veinticinco, ¿cómo lo transformarías en 1000 con dos cuentas? Escribilas
Un estadio está dividido en cuatro sectores como lo indica la imágen y cada uno cuenta con una capacidad de 1000 personas

Respondé
¿Cuál es la capacidad máxima de ambas plateas?
A las 20 hs las dos plateas están llenas y las populares ocupadas sólo hasta la mitad cada una. ¿Cuántos espectadores hay en el estadio en ese momento?
A las 21 horas el estadio está completo. ¿Cuántos espectadores hay?
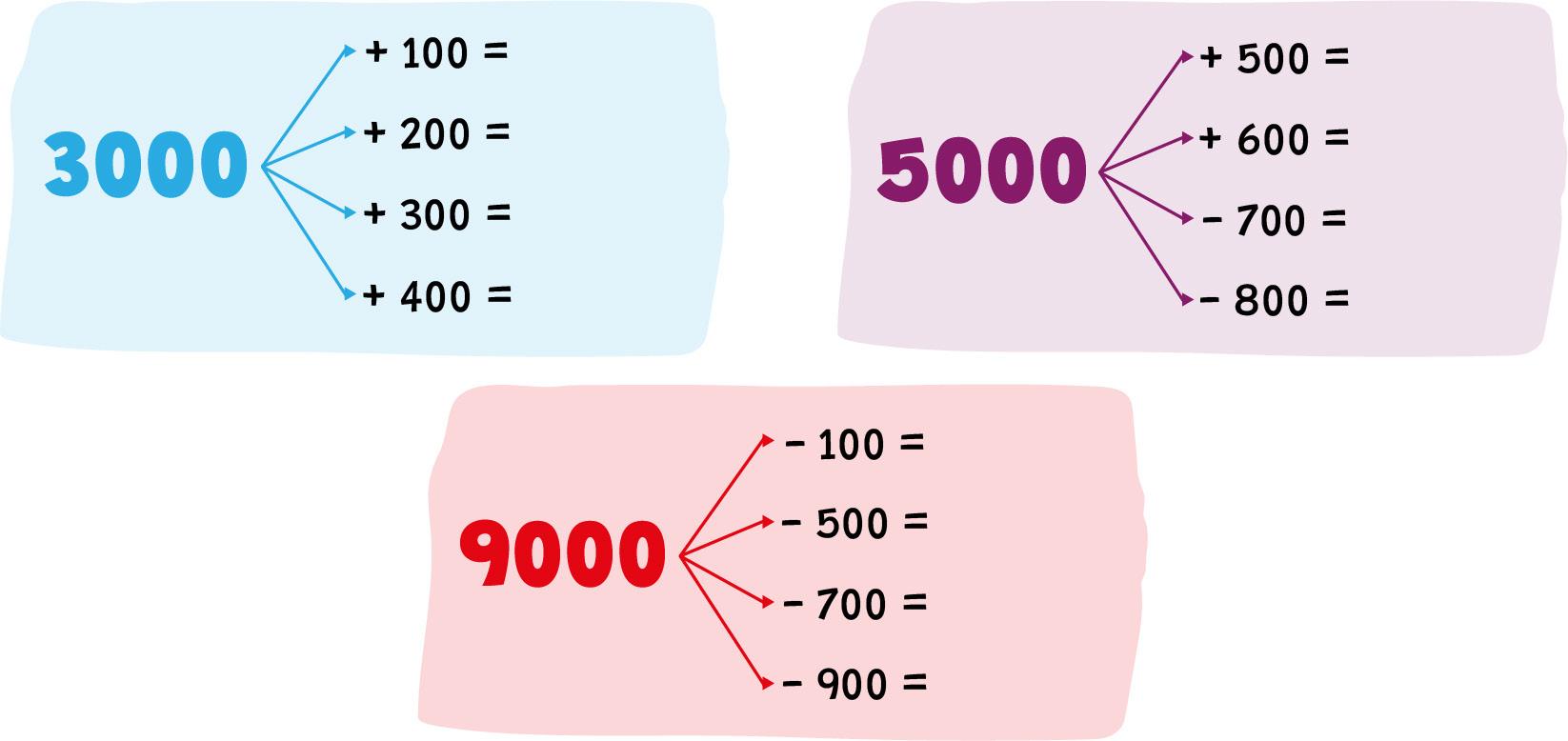
Si en el visor de tu calculadora figura el 9000, usando una sola vez la tecla y una sola vez la tecla , ¿qué cuenta harías para que en el visor apareciera el 3000?

Buscá tres formas distintas de obtener 5000 en el visor de tu calculadora, sin teclearlo directamente. Escribí las diferentes secuencias:
Usando sólo sumas
Usando sólo multiplicación
Usando suma y multiplicación
Escribí qué números salen por la máquina.

Completá cuántas unidades de mil le faltan:
a 1000 para llegar a 9000. Le faltan unidades de mil.
a 2000 para llegar a 8000. Le faltan unidades de mil.
a 1000x2 para llegar a 8000:2. Le faltan unidades de mil.
Completá cómo siguen
Ahora completá
Una escala descendente de a 1000 a partir de 6000
Una escala descendente de a 1000 a partir de 9000
Una escala descendente de a 2000 a partir de 7000
600090007000 -
Durante las vacaciones de invierno, las películas más vistas fueron “Intensamente 2”, “Matilda” y “Encanto”.
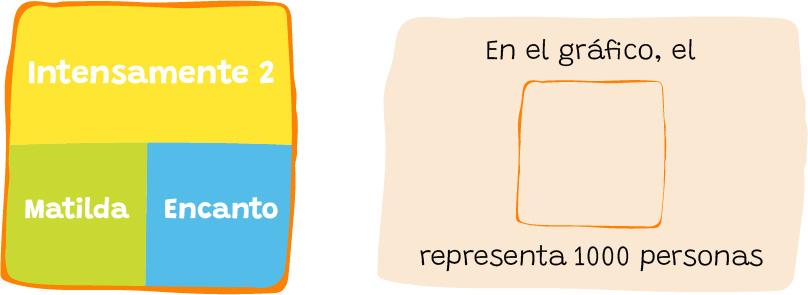
¿Cuántos espectadores vieron Intensamente 2?
¿Cuantas personas en total vieron alguna de las 3 películas?
Resolvé estas operaciones:
900 + 100 =
900 + 10 =
1000 - = 900
El anterior a 1000 es
El número par anterior a 1000 es
Si a 1000 le resto 1 centena tengo
La mitad de 1000 es
La mitad de la mitad de 1000 es
El número impar anterior a 1000 es
Si a 1000 le resto 1 decena tengo
Si a 1000 le resto 1 unidad tengo
Completá
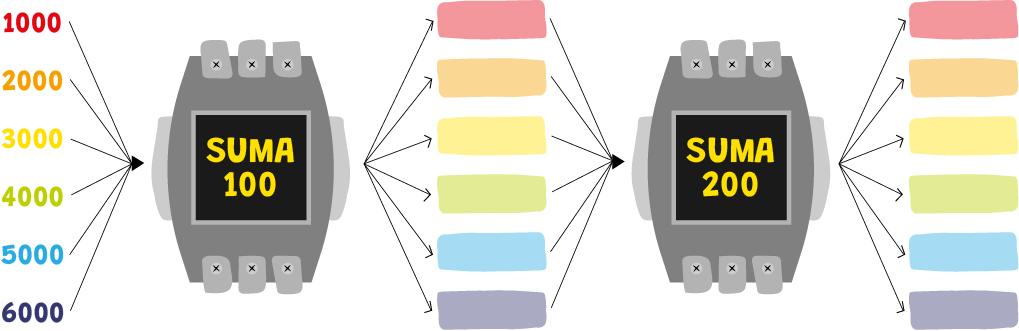
Completá

Escribí el número correspondiente
Cuatro mil doscientos
Novecientos uno
Tres mil cien
Cinco centenas + dos decenas + 3 unidades
Dos unidades de mil + cinco centenas
Cuatro centenas + tres unidades
Encerrá en un círculo los números pares
¿Entre qué unidades de mil, enteras y consecutivas, están los siguientes números?

Ordená los números de forma creciente
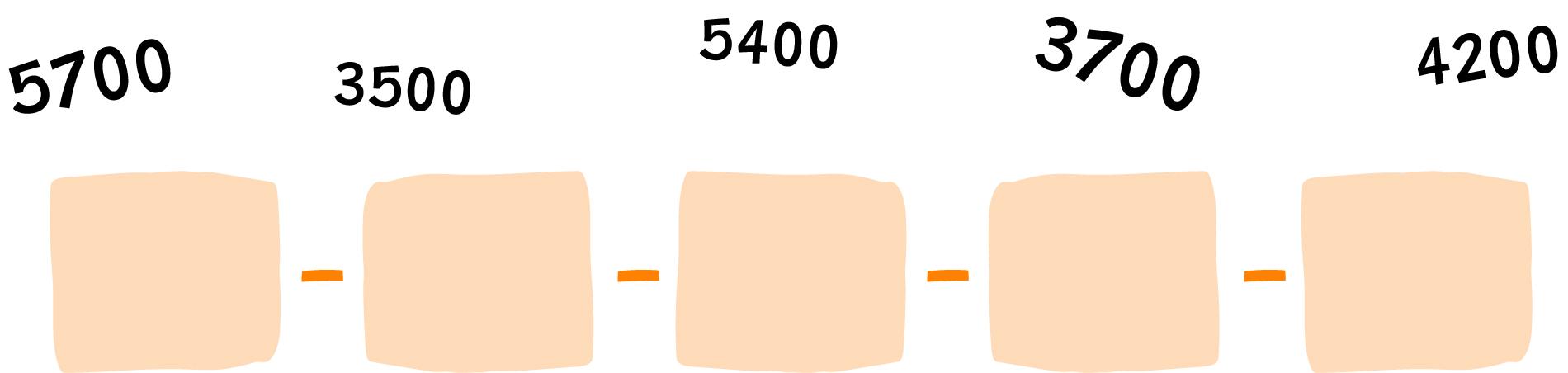
Para llegar a 3 u de mil, ¿cuantas centenas le faltan a: 2500? centenas 1400? centenas 2200? centenas
Calculá 1200 + 800 =
- 1900 =
- 2800 =
x 5 =
x 4 =
: 7 =
: 8 =
: 7 =
: 6 =
Se distribuyen, en cantidades iguales, 1200 libros a 7 bibliotecas.
¿Cuántos libros se envían a cada una?
¿Cuántos quedan por repartir?

Se volaron algunos números de las cuentas, ordená los que corresponden en su lugar.
500
1000 1200 2000 2 3
( 500 x ) - 500 = 1000 ( - 200 ) x 2 = 2000 ( 3000 - 1000 ) - = 0 ( 1300 + 700 ) : = 1
Preparemos los globos
¿Cuántos paquetes de 10 globos cada uno se pueden formar con 1250 globos?
¿Cuántos paquetes de 100 globos cada uno se pueden formar con esa misma cantidad de globos?
¿Cuántas decenas enteras hay en 1250? ¿Y cuantas centenas enteras?
¿Cuál es el resultado de la suma entre
1213 y su inmediato posterior?
2198 y el menor número par que sigue a 1000?
1298 y media docena?

los dos números que faltan en esta sucesión: ?
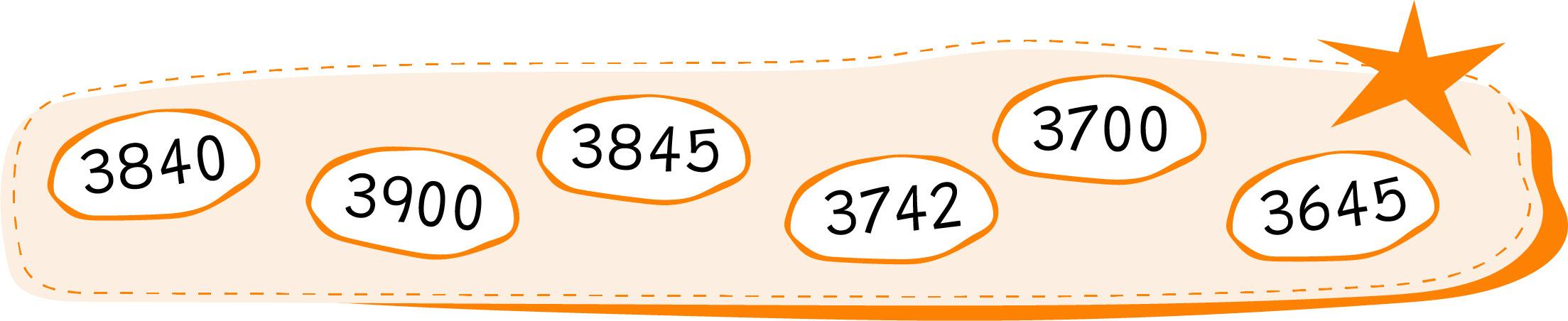
Pintá con verde los números que tienen menos de 384 decenas.
¿Cuál es el menor número que debe sumarse a 5031 para transformarlo en un número par?
¿Qué número obtuviste? Escribilo con palabras.
¿Cuál es el menor número que debe restarse a 4000 para transformarlo en un número impar?
¿Qué número obtuviste? Escribilo con palabras.
Al partido de fútbol de hoy, asisten 5000 personas.
En la popular se acomodan 3000 personas, las demás en la platea, ¿cuántas personas se ubicaron en la platea?
Si en cada fila de la platea se sientan 100 personas, ¿cuántas filas se ocupan?
Siguiendo las pistas, completá los espacios con los dígitos que faltan para formar números de 4 dígitos.
3 7 es el mayor número posible
5 6 es el mayor número posible par
1 5 es el menos impar posible
2 3 > 2938
5348 = 5000 + 300 + 40 +


Juguemos entre todos a encontrar estos objetos en la imágen:
¿Qué forma tiene el dado?
¿Dónde está el globo terráqueo?
¿Cuál fue el camino que recorrió el perrito? Marcalo con color
¿Qué forma tiene la pizarra?
¿En qué columna de la cuadrícula está la manzana?
¿En qué estante está la radio?
¿Y el globo terráqueo?
¿Donde están los lápices?
¿Qué forma tienen los banderines?
¿Qué forma tiene el reloj?
Dibujá 3 dentro de cada figura y 2 fuera de cada una
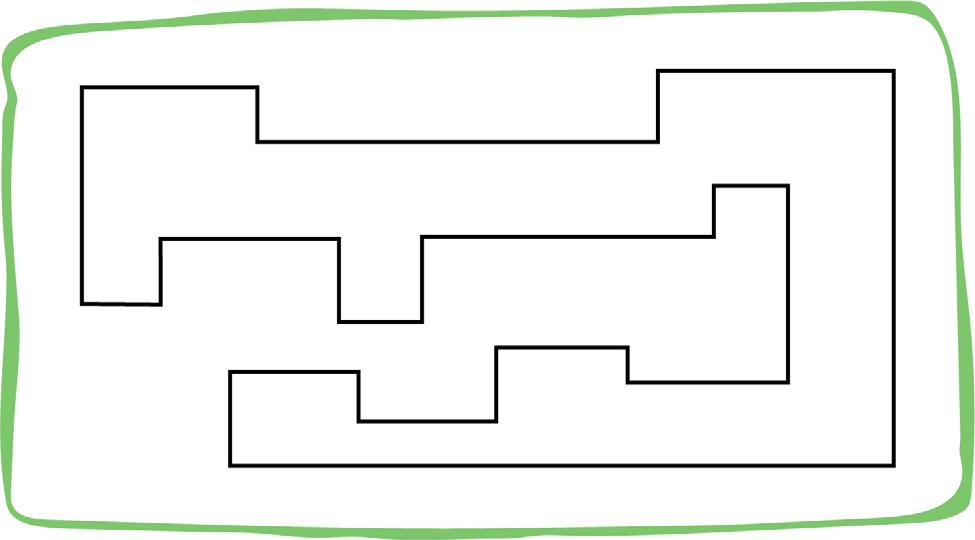
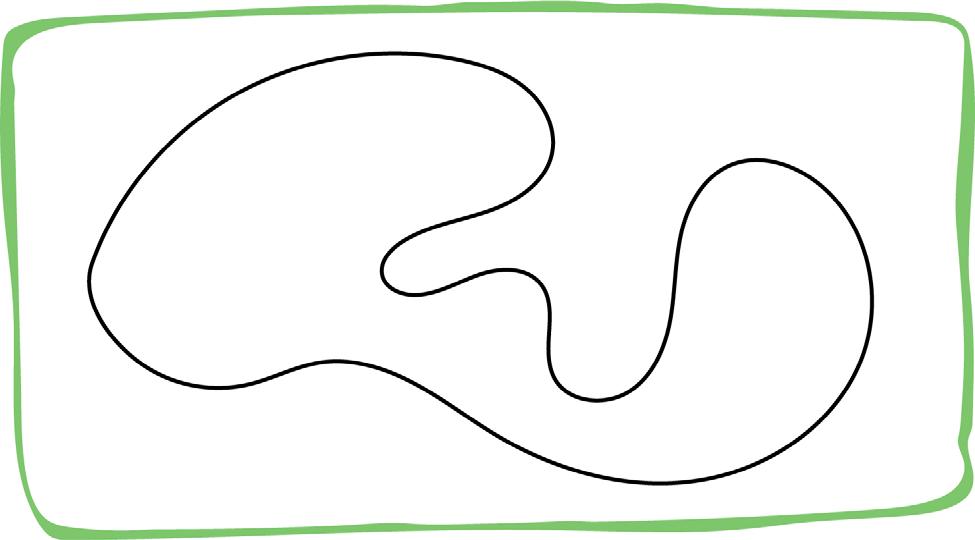
Completá, dibujá y respondé según se indica cada caso.
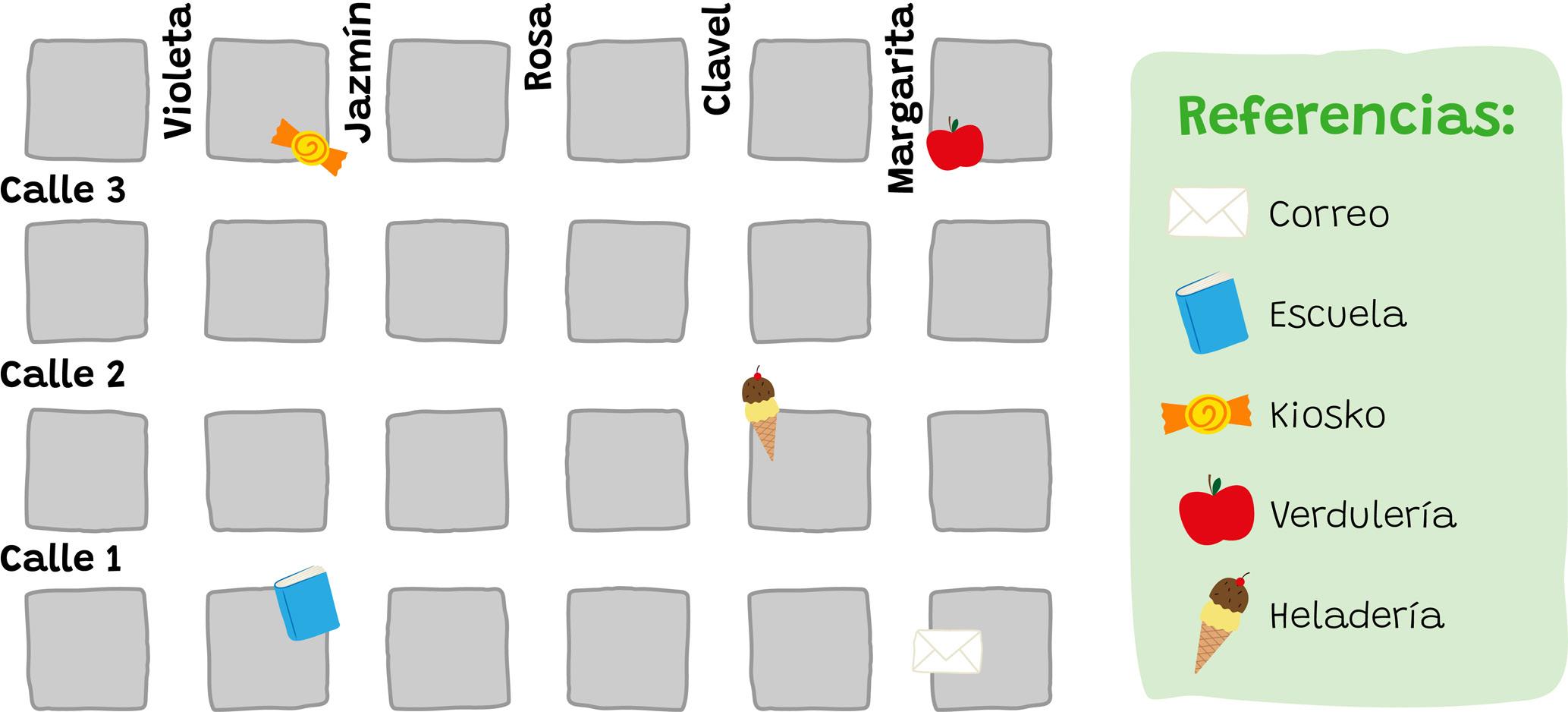
Mirko está en la esquina de Calle 1 y Violeta. Quiere ir a la esquina de Calle 3 y Clavel. ¿Cuál es el menor número de cuadras que tiene que caminar?
¿Cuántas veces dobló?
Belén ha salido de la escuela y quiere comprar golosinas en el kiosko. Ya ha caminado una cuadra por la Calle Rosa hacia el este y quiere caminar lo menos posible por Calle 3. ¿Qué recorrido puede hacer para llegar al kiosko? Trazalo con una línea azul y describilo.
Después de salir del kiosko, Belén se dirige a la heladería.
¿Cuál es el menor número de cuadras que debe caminar para llegar?
¿Cuántas calles cruza en ese caso?
¿Cambia de dirección alguna vez?
Describí la ubicación de la verdulería
Escribí el nombre de las calles que son paralelas a la Calle 1
Coloreá en verde la “Plaza Belgrano” que ocupa toda la manzana comprendida entre las calles Jazmín, Rosa, Calle 1 y Calle 2.
Volvé a observar el plano del barrio y completá
El barrio de Sulino tiene manzanas
La gran mayoría de las calles tienen nombres de
La escuela está ubicada en
Las calles que tienen dirección Norte - Sur se llaman:
Las calles que tienen dirección Este - Oeste se llaman:
Usando flechas indicá el sentido del tránsito de las calles en el plano si:
Las calles Violeta y Rosa van en sentido de Este a Oeste
Las calles 1 y 3 tienen sentido de Norte a Sur
Joaquín llegó al teatro y quiere reservar algunos asientos para sus amigos
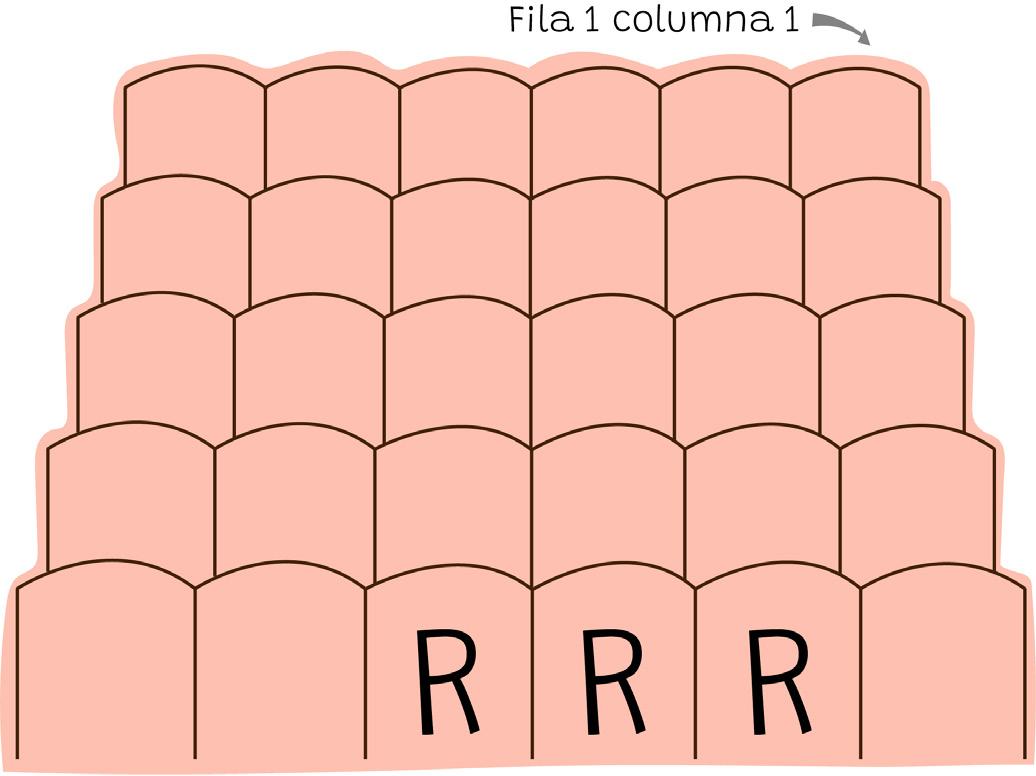
Necesita reservar los siguiente asientos: 3º fila, 4º columna y 3º fila, 5º columna Dibujá una R en los respaldos de dichos asientos.
Hay 3 asientos reservados, ¿qué lugares ocupan?
Busquen un mapa de la ciudad de Rosario y realicen las siguientes actividades:
Ubiquen y marquen:
• El monumento Nacional a la Bandera
• El parque de la Independencia
• La cancha de Rosario Central
• La cancha de Newell´s Old Boys
• La Estación terminal de Ómnibus “Mariano Moreno”
• Los puntos cardinales
¿Con qué limita la ciudad al este?
¿Qué ciudades se encuentran al oeste?
Nombren:
• Dos calles que tengan (aproximadamente) dirección Norte-Sur
• Dos calles que tengan (aproximadamente) dirección Este-Oeste

Uní los puntos negros entre sí de modo que quede formado un cuadrado
Uní los entre sí, de modo que quede formado otro cuadrado
Pintá los triángulos que han quedado formados

Pintá los triángulos de amarillo, los cuadriláteros de azul y los círculos de rojo.
¿Cuántos triángulos hay?
¿Cuántos cuadriláteros?
¿Cuántos círculos?
Ahora, buscá en la FICHA 1, triángulos, rectángulos y círculos, recortalos y creá una figura.
Observá estas figuras de acrílico superpuestas.
¿Qué tipo de figuras son?
Pintá las regiones que quedaron superpuestas. ¿Cuántos triángulos pintaste?
Indicá con una cruz las características que corresponden a este cuerpo geométrico
Tiene 7 caras
Tiene 7 vértices
Tiene 15 aristas
Algunas caras son triangulares
Algunas caras son rectángulos
¿Cuántos triángulos hay? ¿Cuántos rectángulos hay?
Andrés quiere forrar cubos pegando sobre sus caras cuadrados de papel de color. En caras opuestas desea pegar cuadrados de un mismo color pero diferente al de las otras.
¿Cuántos colores distintos usará?
Coloreá cómo podrá verse uno de los cubos forrado.
Si desea forrar 6 cubos iguales a éste, ¿cuántos cuadrados de cada color necesita?
¿Qué dos propiedades comunes descubris de cada par de figuras?

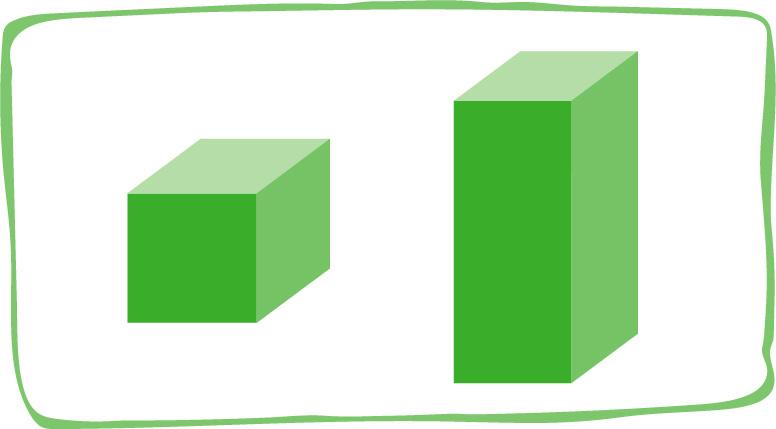
¿Con cuáles de estos desarrollos planos podrías armar una pirámide de base cuadrada? Marcalo con una cruz.
Coloreá con marrón los triángulos, con rojo los cuadriláteros y con azul los pentágonos.
¿Quedaron polígonos sin pintar? ¿Cómo se llaman?
En la FICHA 3 encontrarás figuras como las anteriores. Recortá los cuadriláteros y plegándolos descubrí si tienen algún eje de simetría. Pegá los que lo tengan, marcando sus ejes con distinto color en caso de encontrar más de uno.
Marcá con una cruz la opción correcta en cada caso.
Un hexágono tiene:
4 vértices
5 vértices
6 vértices
Ninguna de las anteriores
Un pentágono tiene:
4 diagonales
5 diagonales
6 diagonales
Ninguna de las anteriores

¿Cuál de las siguientes figuras tiene un eje de simetría?
Un a pirámide de base cuadrada tiene:
4 caras
5 caras
6 caras
Ninguna de las anteriores
Un cuadrado tiene:
1 eje de simetría
2 ejes de simetría
3 ejes de simetría
Ninguna de las anteriores
¿Cuántos pares de rectas paralelas hay en esta figura?
¿Cuántos triángulos hay en esta figura?
Ninguna de las anteriores
¿Cuáles son calles perpendiculares?
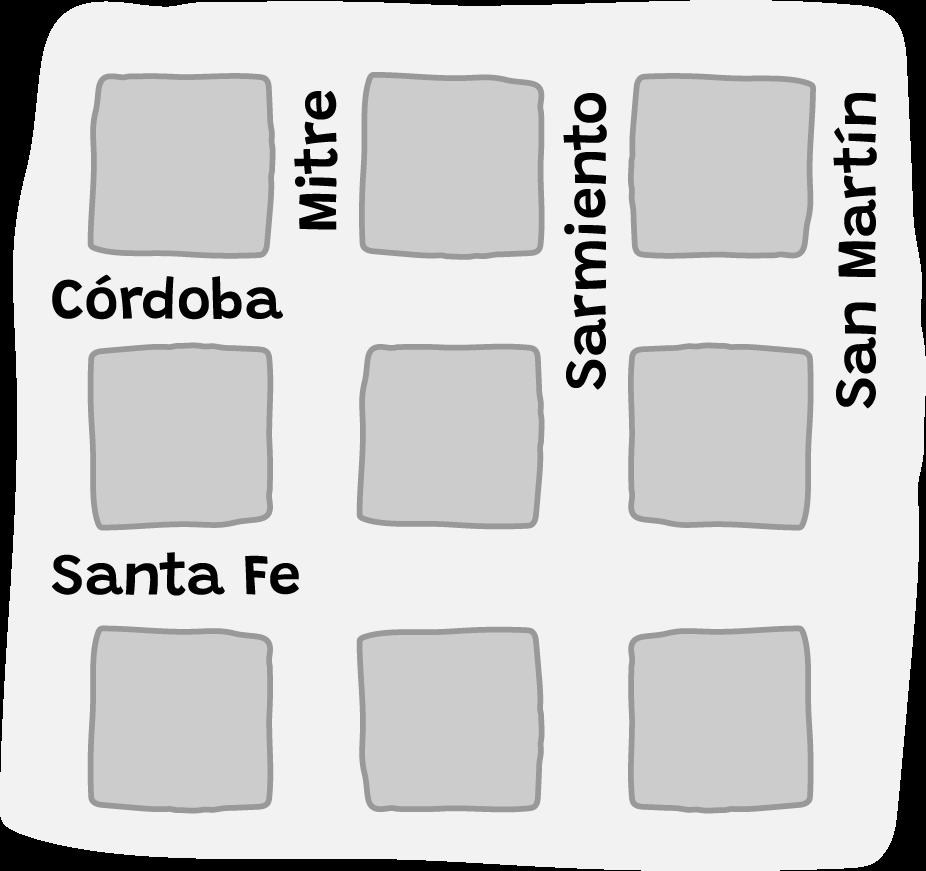
San Martín y Sarmiento
Mitre y Santa Fe
Córdoba y Santa Fe
Mitre y San Martín










