168
Capítulo 3
Aplicaciones de la derivada
Encontrar el extremo absoluto En los ejercicios 41 a 44, utilice una herramienta de graficación para trazar la gráfica de la función y determine los extremos absolutos de la misma en el intervalo indicado. 41. f x 43. f x
3 x
1
x4
44. f x
,
2x3
x
x cos , 2
x
2
42. f x
1, 4 1,
2
x
,
0, 2
1, 3
0, 2
Encontrar extremos usando la tecnología En los ejercicios 45 y 46, (a) use un sistema de álgebra por computadora para representar la función y aproximar cualquier extremo absoluto en el intervalo dado. (b) Utilice una herramienta de graficación para determinar cualquier punto crítico y use éstos para encontrar todos los extremos absolutos no ubicados en los puntos finales. Compare los resultados con los del inciso (a). 45. f x
3.2x 5
5x 3
46. f x
4 x 3 3
x,
3.5x,
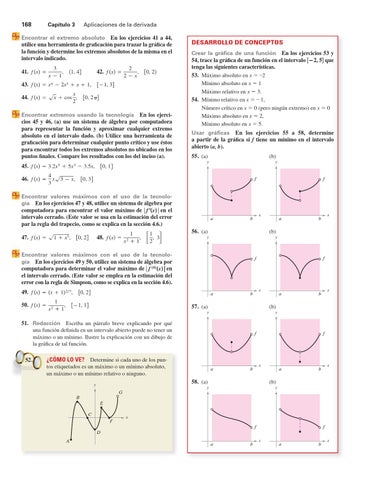
DESARROLLO DE CONCEPTOS Crear la gráfica de una función En los ejercicios 53 y 54, trace la gráfica de un función en el intervalo [ 2, 5] que tenga las siguientes características. 53. Máximo absoluto en x = –2 Mínimo absoluto en x = 1 Máximo relativo en x = 3. 54. Mínimo relativo en x = – 1, Número crítico en x = 0 (pero ningún extremo) en x = 0 Máximo absoluto en x = 2, Mínimo absoluto en x = 5. Usar gráficas En los ejercicios 55 a 58, determine a partir de la gráfica si f tiene un mínimo en el intervalo abierto (a, b). 55. (a)
(b)
y
y
0, 1
0, 3
Encontrar valores máximos con el uso de la tecnología En los ejercicios 47 y 48, utilice un sistema de álgebra por computadora para encontrar el valor máximo de f x en el intervalo cerrado. (Este valor se usa en la estimación del error par la regla del trapecio, como se explica en la sección 4.6.) 47. f x
x3,
1
1
48. f x
0, 2
x2
1
,
1 , 3 2
a
50. f x
x 1 x2
2 3
1 1
,
,
(b)
y
y
f
x
b
a
57. (a)
(b)
y
y
51. Redacción Escriba un párrafo breve explicando por qué una función definida en un intervalo abierto puede no tener un máximo o un mínimo. Ilustre la explicación con un dibujo de la gráfica de tal función.
a
f
x
b
x
b
f
¿CÓMO LO VE? Determine si cada uno de los puntos etiquetados es un máximo o un mínimo absoluto, un máximo o un mínimo relativo o ninguno.
x
b
f
a
y
a
56. (a)
0, 2 1, 1
x
b
Encontrar valores máximos con el uso de la tecnología En los ejercicios 49 y 50, utilice un sistema de álgebra por computadora para determinar el valor máximo de f 4 x en el intervalo cerrado. (Este valor se emplea en la estimación del error con la regla de Simpson, como se explica en la sección 4.6). 49. f x
f
f
a
58. (a)
(b)
y
y
x
b
G B E C F
x
f
f
D A
a
b
x
a
b
x